
����Ŀ��������̽��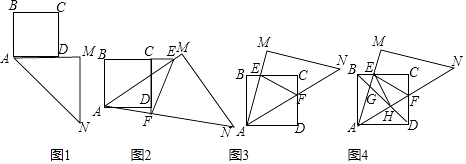
�ۺ�ʵ���Σ���ʦ��һ���㹻��ĵ���ֱ�����dz�AMN����һ��������ֽƬABCD��һ�࣬ʹ��AM��AD��ͬ
һֱ���ϣ���ͼ1�������С�AMN=90�㣬AM=MN��
��1�����뷢��
��ʦ�����dz�AMN�Ƶ�A��ʱ����ת������ͼ2����0������45��ʱ����AM��AN�ֱ���ֱ��BC��CD���ڵ�E��F������EF��С��ͬѧ̽�����֣��߶�EF��BE��DF����EF=BE��DF����ͼ3����45�㣼����90��ʱ�������������䣮
����գ���DAF+��BAE=�ȣ�
�ڲ��룺�߶�EF��BE��DF����֮���������ϵ�ǣ� ��
��2��֤����IJ��룻
��3����չ̽��
��45�㣼����90��������£�����BD���ֱ�AM��AN�ڵ�G��H����ͼ4����EH����֤����EH��AN��
���𰸡�
��1��45,EF=BE+DF
��2���⣺֤������ͼ3���ӳ�CB����K��ʹBK=DF������AK��
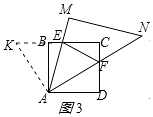
���ı���ABCD�������Σ�
��AB=AD����BAD=��ABK=��D=90�㣮
�ڡ�ABK�͡�ADF�У� 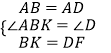 ��
��
���ABK�ա�ADF��SAS����
��AK=AF����BAK=��DAF��
�ߡ�AMN=90�㣬AM=MN��
���MAN=��N=45�㣬
���DAF+��BAE=45�㣮
���EAK=��BAK+��BAE=45�㣬
���EAF=��EAK��
�ڡ�AEF�͡�AEK�У� 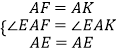 ��
��
���AEF�ա�AEK��SAS����
��EF=EK��
��EF=BE+DF��
��3���⣺֤������ͼ4������AC��
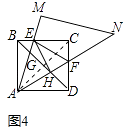
���ı���ABCD�������Σ�
���ACE=��ADH=��CAD=45�㣮
�ߡ�EAF=45�㣬
���EAF=��CAD=45�㣮
���CAE=��DAH��
���ADH�ס�ACE��
�� ![]() ��
��
�� ![]() ��
��
�֡ߡ�CAD=��EAF=45�㣬
���ADC�ס�AHE��
���ADC=��AHE=90�㣮
��EH��AN��
����������1���⣺�١�DAF+��BAE=45�㣻
���Դ��ǣ�45�����߶�EF��BE��DF����֮���������ϵ��EF=BE+DF��
���Դ��ǣ�EF=BE+DF��
�����㾫�������������ε����ʺ����������ε��ж������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
�ڽ�����3|x-2|=|x-2|+4��һ�ຬ�о���ֵ�ķ���ʱ�����ǿ��Ը��ݾ���ֵ�������x��2��x��2����������ۣ�
�ٵ�x��2ʱ��ԭ���̿ɻ�Ϊ-3��x-2��=-��x-2��+4����ã�x=0������x��2
�ڵ�x��2ʱ��ԭ���̿ɻ�Ϊ3��x-2��=��x-2��+4����ã�x=4������x��2
��ԭ���̵Ľ�Ϊ��x=0��x=4��
����عˣ�������2Ϊx-2����㣬���������ϵĵ�����Ӧ�����ֳ���x��2��x��2�����֣����Է�x��2��x��2����������ۣ�
֪ʶǨ�ƣ�
��1����������˼������|x-3|��ֵ����ȥ����ֵ���ŵķ����ⷽ�̣�|x-3|+8=3|x-3|��
֪ʶӦ�ã�
��2�����÷���������ȥ����ֵ���ŵķ��������Ƶķ��̣�|2-x|-3|x+1|=x-9��
����ʾ����������������㣬���ǰ������ϵĵ�����Ӧ�����ֳ��˼������أ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����D����ABC�ڣ���EΪ��BC��һ�㣬����DE��CD��
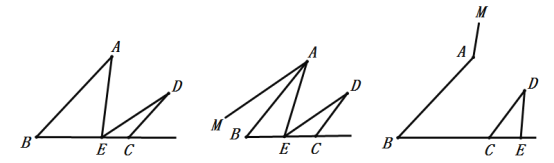
��1����ͼ1������AE������AED=��A+��D����֤��AB//CD��
��2���ڣ�1���Ľ����£�����A��ֱ��MA//ED��
����ͼ2������E���߶�BC��ʱ�����벢��֤��MAB����CDE��������ϵ��
����ͼ3������E���߶�BC���ӳ�����ʱ�����벢��֤��MAB����CDE��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=kx+2�뷴��������y2= ![]() ��ͼ���ڵ�A��m��3������������ֱ���B��C���㣮
��ͼ���ڵ�A��m��3������������ֱ���B��C���㣮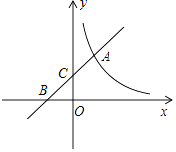
��1����y1��y2��0�����Ա���x��ȡֵ��Χ��
��2������P��n��0����x�����˶�����nΪ��ֵʱ��|PA��PC|��ֵ��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() ������ƽ��ֱ������ϵ�У���֪��
������ƽ��ֱ������ϵ�У���֪��![]() ����
����![]() ������
������![]() ��
��![]() ��������
��������![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���ͬʱ������
����λ���ٶ��˶���ͬʱ������![]() ��
��![]() ��������
��������![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���������һ�㵽��
����λ���ٶ��˶���������һ�㵽��![]() ��ʱ��������ͬʱֹͣ�˶����˶�ʱ��Ϊ
��ʱ��������ͬʱֹͣ�˶����˶�ʱ��Ϊ![]() ��
��

��1����![]() ______ʱ����
______ʱ����![]() �ϵ�
�ϵ�![]() ����ʱ��
����ʱ��![]() ������Ϊ_______��
������Ϊ_______��
��2����![]() ʱ���ֱ�ȡ
ʱ���ֱ�ȡ![]() ��
��![]() ���е�
���е�![]() ��
��![]() ������ı���
������ı���![]() ���������
���������![]() �������ʱ��
�������ʱ��![]() ��ȡֵ��
��ȡֵ��
��3����ͼ2������![]() ����֪
����֪![]() ���ڣ�2���ʵ������£�����
���ڣ�2���ʵ������£�����![]() ��
��![]() �ڵ�
�ڵ�![]() �����ڳ�����
�����ڳ�����![]() �����������Ƿ���ڵ�
�����������Ƿ���ڵ�![]() ��ʹ���߶�
��ʹ���߶�![]() �������ڣ���ֱ��д����
�������ڣ���ֱ��д����![]() �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABOC�Ķ���O������ԭ�㣬��BO��x��ĸ������ϣ���BOC=60�㣬����C������Ϊ��m��3 ![]() ��������������y=
��������������y= ![]() ��ͼ�������ζԽ���AO��D�㣬����BD����DB��x��ʱ��k��ֵ�ǣ� ��
��ͼ�������ζԽ���AO��D�㣬����BD����DB��x��ʱ��k��ֵ�ǣ� ��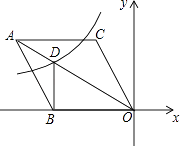
A.6 ![]()
B.��6 ![]()
C.12 ![]()
D.��12 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨����a��b֮���һ�����㣬����(a��b)�����![]() ��
��![]() ��ô(a��b)=c��
��ô(a��b)=c��
���磺��Ϊ23=8������(2��8)=3��
(1)���������涨����գ�
��3��9��=_____����5��125��=_____����![]() ��
��![]() ��=_____����-2��-32��=_____��
��=_____����-2��-32��=_____��
(2)��![]() ��
��![]() ��
��![]() ����˵�����е�ʽ���������ɣ�
����˵�����е�ʽ���������ɣ�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1�����㣺��3���У�0+4sin45�㩁 ![]() +|1��
+|1�� ![]() |
|
��2��������ֵ���� ![]() +
+ ![]() ����
���� ![]() ������x=6��
������x=6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ����4500Ԫ����һ���������ܿ����꣬��װ���ϰ�����2100Ԫ�����ڶ����ÿ�ʽ�ij������������ǵ�һ�ε�һ�룬������ÿ���ȵ�һ��������10Ԫ��
��1�������θ��������ֳ������ټ���
��2������һ���������ۼ���200Ԫ/�����ϰ�����������������������������1950Ԫ����ڶ�������ÿ������Ҫ�۶���Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com