
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E. 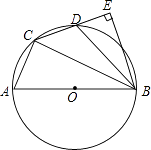
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB= ![]() ,求OE的长度.
,求OE的长度. 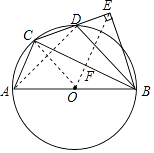
【答案】
(1)解:连接AD,

∵D为弧AB的中点,
∴AD=BD,
∵AB为直径,
∴∠ADB=90°,
∴∠DAB=∠DBA=45°,
∴∠DCB=∠DAB=45°
(2)解:证明:∵BE⊥CD,又∵∠ECB=45°,
∴∠CBE=45°,
∴CE=BE,
∵四边形ACDB是圆O的内接四边形,
∴∠A+∠BDC=180°,
又∵∠BDE+∠BDC=180°,
∴∠A=∠BD,
又∵∠ACB=∠BED=90°,
∴△ABC∽△DBE,
∴DE:AC=BE:BC,
∴DE:BE=AC:BC=1:2,
又∵CE=BE,
∴DE:CE=1:2,
∴D为CE的中点
(3)解:∵CO=BO,CE=BE,
∴OE垂直平分BC,
∴F为BC中点,
又∵O为AB中点,
∴OF为△ABC的中位线,
∴OF= ![]() AC,
AC,
∵∠BEC=90°,EF为中线,
∴EF= ![]() BC,
BC,
在Rt△ACB中,AC2+BC2=AB2,
∵AC:BC=1:2,AB= ![]() ,
,
∴AC= ![]() ,BC=2
,BC=2 ![]() ,
,
∴OE=OF+EF=1.5 ![]() .
.
【解析】(1)连接AD,由D为弧AB的中点,得到AD=BD,根据圆周角定理即可得到结论;(2)由已知条件得到∠CBE=45°,根据圆内接四边形的性质得到∠A=∠BD,根据相似三角形的性质得到DE:AC=BE:BC,即可得到结论.(3)连接CO,根据线段垂直平分线的判定定理得到OE垂直平分BC,由三角形的中位线到现在得到OF= ![]() AC,根据直角三角形的性质得到EF=
AC,根据直角三角形的性质得到EF= ![]() BC,由勾股定理即可得到结论.
BC,由勾股定理即可得到结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
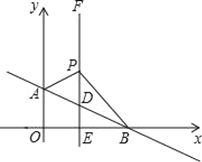
【题目】如图,平面直角坐标系中,直线AB:y=﹣![]() x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
(1)直线AB的表达式为__________________;
(2)①求△ABP的面积(用含n的代数式表示);
②当S△ABP=2时,求点P的坐标;
③在②的条件下,以PB为边在第一象限作等腰直角三角形BPC,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如:![]() ,
,![]() =3.
=3.
(1)仿照以上方法计算:![]() =______;
=______;![]() =_____.
=_____.
(2)若![]() ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次![]()
![]()
![]() =1,这时候结果为1.
=1,这时候结果为1.
(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种数量与3月份相同,4月份共收取运费13000元.试求该物流公司月运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
科目:初中数学 来源: 题型:
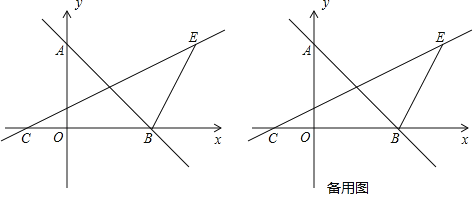
【题目】如图,一次函数y=﹣x+4的图象与y轴交于点A,与x轴交于点B,过AB中点D的直线CD交x轴于点C,且经过第一象限的点E(6,4).
(1)求A,B两点的坐标及直线CD的函数表达式;
(2)连接BE,求△DBE的面积;
(3)连接DO,在坐标平面内找一点F,使得以点C,O,F为顶点的三角形与△COD全等,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】脸谱是中国戏曲男演员脸部的彩色化妆.这种脸部化妆主要用于净(花脸)和丑(小丑),表现人物的性格和特征.现有四张脸谱,如图所示:有两张相同的表现忠勇侠义的净角姜维,有一张表现直爽刚毅的净角包拯,有一张表现阴险奸诈的丑角夏侯婴. 
(1)随机抽取一张,获得一张净角脸谱的概率是;
(2)随机抽取两张,求获得一张姜维脸谱和一张包拯脸谱的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com