
【题目】如图1,点E是正方形ABCD的边CD上一点(不与C、D重合),连接AE,过点A作AF⊥AE交CB的延长线于点F
(1)求证:AE=AF;
(2)连接EF,N为EF之中点,连接BN,求![]() 的值;
的值;
(3)以BF为边作正方形BFMH,如图2,CH与AF相交于点Q,当E在CD上运动(不与C、D重合),问∠CQD的大小是否发生变化?若不变,求其值;若变化,请指出其范围.
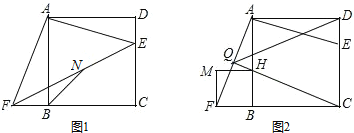
【答案】(1)见解析;(2)![]() ;(3)不变,45°.
;(3)不变,45°.
【解析】
(1)由四边形ABCD是正方形,得到AB=AD,∠ABC=∠BAD=∠D=90°,∠ABF=90°,因为∠FAE=90°,所以∠FAE-∠BAE=∠BAD-∠BAE,即;∠FAB=∠EAD,得到△ABF≌△DAE,求出AF=AE;
(2)取FC的中点N,连接MN,AM,因为点M是FE的中点,得到CE=2MN,由∠AKM=∠FKB,∠AMF=∠MNB=90°,得到△AKM∽△BKM,![]() ,因为∠AKB∠=MKB,所以△AFK∽△BKF,得到∠KBM=∠AFK=45°,∠MBN=45°,所以BM=
,因为∠AKB∠=MKB,所以△AFK∽△BKF,得到∠KBM=∠AFK=45°,∠MBN=45°,所以BM=![]() MN,
MN,![]() ;
;
(3)过点D作DQ⊥PD交PC的延长线于Q,由四边形BFHG是正方形,得到BG=BF,所以△ABF≌△CBG,∠FAB=∠BCG,由∠AGP=∠CGB,得到∠APG=∠ABC=90°,因为∠ADC=∠PDQ=90°,得到∠ADP=∠QDC,由AB∥CD,得到∠DCQ=∠AGC,∠PAG+∠BAD=∠PAG+∠APG,即∠PAD=∠AGC=∠DCQ,得到△PAD≌△QCD(ASA),PD=DQ,∠DPQ=45°,得出∠APD=45°.
(1)证明:∵AF⊥AE,∠BAD=90°,
∴∠FAB=∠EAD,
在△FAB和△EAD中,
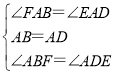 ,
,
∴△FAB≌△EAD,
∴AE=AF;
(2)如图1,连接AN,作NM⊥BC于M,则NM∥CD,
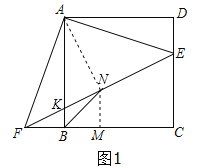
又点N是FE的中点,
∴CE=2MN,
∵∠AKN=∠FKB,∠ANK=∠FBK=90°,
∴△AKN∽△FKB,
∴![]() ,
,
又∠AKF=∠NKB,
∴△AKF∽△NKB,
∴∠NBK=∠AFK=45°,
∴∠NBM=45°,
∴BN=![]() MN,
MN,
∴![]() ;
;
(3)如图2,过点D作DR⊥QD交BC的延长线于R,
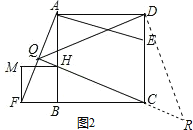
∵四边形BFMH是正方形,
∴BH=BF,
在△ABF与△CBH中,
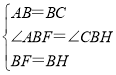 ,
,
∴△ABF≌△CBH,
∴∠BAF=∠BCH,又∠AHQ=∠CHB,
∴∠AQH=∠ABC=90°,
∵∠AHC=∠AQH+∠BAF,∠QAD=∠BAF+∠BAD,
∴∠AHC=∠QAD,
∵AB∥CD,
∴∠AHC=∠DCR,
∴∠DCR=∠QAD,
∵∠ADC=∠QDR=90°,
∴∠ADQ=∠CDR,
在△QAD和△DCR中,
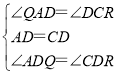 ,
,
∴△QAD≌△RCD,
∴DQ=DR,
∴∠CQD=45°.


科目:初中数学 来源: 题型:
【题目】已知:![]() 为直线
为直线 ![]() 上的一点,以
上的一点,以![]() 为观察中心,射线
为观察中心,射线![]() 表示正北方向,
表示正北方向,![]() 表示正东方向(即
表示正东方向(即![]() ),射线
),射线![]() ,射线
,射线![]() 的方向如各图所示.
的方向如各图所示.
(1)如图1所示,当 ![]() 时:
时:
①若![]() ,则射线
,则射线![]() 的方向是 .
的方向是 .
② ![]() 与
与![]() 的关系为 ,
的关系为 ,
③ ![]() 与
与![]() 的关系为 .
的关系为 .
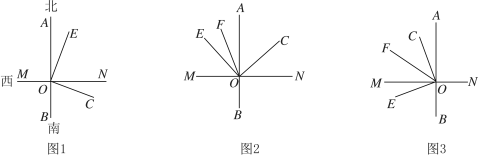
(2)若将射线![]() ,射线
,射线![]() 绕点
绕点![]() 旋转至图
旋转至图![]() 的位置,另一条射线
的位置,另一条射线![]() 恰好平分
恰好平分![]() ,旋转中始终保持
,旋转中始终保持![]() .
.
①若![]() ,则
,则![]() 度 .
度 .
②若![]() ,则
,则![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
(3)若将射线![]() ,射线
,射线![]() 绕点
绕点![]() 旋转至图
旋转至图![]() 的位置,射线
的位置,射线![]() 仍然平分
仍然平分![]() ,旋转中始终保持
,旋转中始终保持![]() ,则
,则![]() 与
与![]() 之间存在怎样的数量关系,并说明理由.
之间存在怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
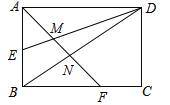
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织员工去公园划船,报名人数不足50人,在安排乘船时发现,每只船坐6人,剩下18人无船可乘;每只船坐10人,那么其余的船坐满后,有一只船不空也不满,参加划船的员工共有( )
A.48人B.45人C.44人D.42人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是四边形
分别是四边形![]() 边
边![]() 、
、![]() 、
、![]() 、
、![]() 的中点.则下列说法:①若
的中点.则下列说法:①若![]() ,则四边形
,则四边形![]() 为矩形;②若
为矩形;②若![]() ,则四边形
,则四边形![]() 为菱形;③若四边形
为菱形;③若四边形![]() 是平行四边形,则
是平行四边形,则![]() 与
与![]() 互相平分;④若四边形
互相平分;④若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 互相垂直且相等.其中正确的个数是( )
互相垂直且相等.其中正确的个数是( )
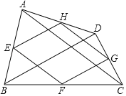
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,如图是购买甲、乙两家商场该商品的实际金额![]() 、
、![]() (元)与原价
(元)与原价![]() (元)的函数图象,下列说法正确的是( )
(元)的函数图象,下列说法正确的是( )
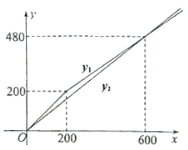
A. 当![]() 时,选甲更省钱B. 当
时,选甲更省钱B. 当![]() 时,甲、乙实际金额一样
时,甲、乙实际金额一样
C. 当![]() 时,选乙更省钱D. 当
时,选乙更省钱D. 当![]() 时,选甲更省钱
时,选甲更省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.

(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
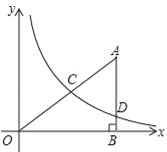
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备在国庆节期间组织学生到泰山进行研学旅行,已知老师与学生一共25人参加此次研学旅行,购买门票共花费1700元,门票费用如表格所示,求参加研学旅行的老师和学生各有多少人?设老师有x人,学生有y人,则可列方程组为( )
景点 | 票价 | 开放时间 |
泰山门票 | 旺季:125元/人 淡季:100元/人 | 全天 |
说明:(1)旺季时间(2月~11月),淡季时间(12月-次年1月); (2)老年人(60岁~70岁)、学生、儿童(1.2米~1.4米)享受5折优惠; (3)教师、省部级劳模、英模、道德模范享受8折优惠; (4)现役军人、伤残军人、70岁以上老年人、残疾人,凭本人有效证件免费进山; (5)享受优惠的游客请出示本人有效证件。 | ||
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com