练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

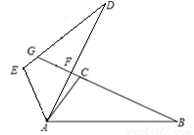
    （10分）如图所示，△ABC≌△ADE，且∠CAD=10°，∠D=25°，∠EAB=120°，求∠DFB的度数．

    【解析】
    ∵△ABC≌△ADE，∠D=25°

    ∴∠B=∠D=25°

    ∠EAD=∠CAB

    ∵∠EAB=∠EAD+∠CAD+∠CAB=120°

    ∠CAD=10°

    ∴∠CAB= ×（120°-10°）=55°

    ∴∠FAB=∠CAB+∠CAD=55°+10°=65°

    又∵∠DFB是△ABF的外角

    ∴∠DFB=∠B+∠FAB

    ∴∠DFB=25°+65°=90°

    【解析】

    试题分析：由△ABC≌△ADE，可得∠EAD=∠CAB，根据已知条件可求得∠FAB的度数，再根据三角形外角性质可得∠DFB=∠FAB+∠B，即可求得∠DFB的度数.

    考点：全等三角形的性质，三角形的外角性质.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年重庆市八年级上学期期末模拟数学试卷（解析版） 题型：填空题

    如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，且DE=2CE，过点C作CF⊥BE，垂足为F，连接OF，则OF的长为 ．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省慈溪市八年级12月评估测试数学试卷（解析版） 题型：解答题

    （本题12分）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E．证明:DE=BD+CE．

    （2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=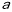,其中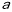为任意锐角或钝角．请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由．

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省慈溪市八年级12月评估测试数学试卷（解析版） 题型：选择题

    如图，在锐角△ABC中，AB=6，∠BAC=60°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（ ）

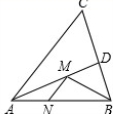
    A．3 B． C． D．6

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省慈溪市八年级12月评估测试数学试卷（解析版） 题型：选择题

    不等式1＋x＜0的解集在数轴上表示正确的是（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年新疆伊宁市八年级上学期期中考试数学试卷（解析版） 题型：填空题

    如图所示，已知在△ABC中，∠A=90°，AB=AC，CD平分∠ACB，DE⊥BC于E，若BC=12 cm，则△DEB的周长为______cm。

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年新疆伊宁市八年级上学期期中考试数学试卷（解析版） 题型：填空题

    若三角形两条边长分别为6cm和4cm，且第三边长为偶数，则周长为

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年新疆克拉玛依市八年级上学期期末考试数学试卷（解析版） 题型：填空题

    当x＝__________时，分式无意义．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年四川省广安岳池白庙督导区八年级10月月考数学试卷（解析版） 题型：解答题

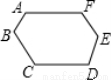
    如图,一个六边形的六个内角都是120°,AB=1,BC=CD=3,DE=2,求该六边形的周长.（8分）

    查看答案和解析>>

    同步练习册答案