
分析 (1)根据题意可以求得降价前服装店每天销售该服装可获的利润;
(2)根据题意可以列出相应的方程,从而可以求得每件服装应降的钱数,注意要使顾客得到更多的实惠;
(3)根据题意可以得到利润与降价的函数关系式,然后化为顶点式,即可解答本题.
解答 解:(1)由题意可得,
降价前服装店每天销售该服装可获利:(100-60)×20=40×20=800(元),
即降价前服装店每天销售该服装可获利800元;
(2)设每件服装降价x元,
(100-60-x)(20+2x)=1200,
解得,x1=10,x2=20,
∵要使顾客得到更多的实惠,
∴每件服装应降价20元;
(3)设每件服装降价x元,利润为W元,
W=(100-60-x)(20+2x)=-2(x-15)2+1250,
∴当x=15时,W取得最大值,此时W=1250,
即每件服装降价15元服装店可获得最大利润,最大利润是1250元.
点评 本题考查二次函数的应用,一元二次方程的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,列出相应的方程或函数关系式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 甲班 | B. | 乙班 | C. | 两班一样整齐 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3和$\sqrt{(-3)^{2}}$ | B. | $\sqrt{(-3)}$和-$\frac{1}{3}$ | C. | -3和$\root{3}{-27}$ | D. | $\root{3}{27}$和|-3| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
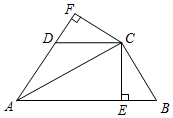 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com