
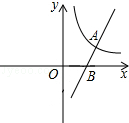
 如图,直线y=2x-6与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A(4,2),与x轴交于点B.
如图,直线y=2x-6与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A(4,2),与x轴交于点B.分析 (1)根据点的坐标利用反比例函数图象上点的坐标特征即可求出k值,再令直线y=2x-6中y=0求出x的值,即可得出点B的坐标;
(2)联立一次函数与反比例函数解析式成方程组,求出另一交点坐标,补充完整函数图象,根据两函数图象的上下位置关系即可得出结论;
(3)假设存在,设点C的坐标为(m,0),由两点间的距离公式分别表示出AB、AC的长度,令AC=AB,即可得出关于m的无理方程,解方程即可得出结论.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$(k>0)的图象过点A(4,2),
∴k=4×2=8,
∴反比例函数的解析式为y=$\frac{8}{x}$.
令y=2x-6中y=0,则2x-6=0,
解得:x=3,
∴点B的坐标为(3,0).
(2)联立两函数的解析式成方程组,
得:$\left\{\begin{array}{l}{y=\frac{8}{x}}\\{y=2x-6}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=-8}\end{array}\right.$,或$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$.
补充完整函数图象,如图所示.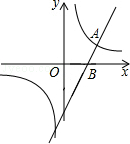
观察两函数图象可发现:当-1<x<0或x>4时,一次函数图象在反比例函数图象的上方,
∴不等式2x-6>$\frac{k}{x}$(k>0)的解集为-1<x<0或x>4.
故答案为:-1<x<0或x>4.
(3)假设存在,设点C的坐标为(m,0),
则AB=$\sqrt{(4-3)^{2}+(2-0)^{2}}$=$\sqrt{5}$,AC=$\sqrt{(4-m)^{2}+(2-0)^{2}}$,BC=|m-3|.
∵△ABC为等腰三角形,且AC=AB,
∴$\sqrt{5}$=$\sqrt{(4-m)^{2}+(2-0)^{2}}$,即(4-m)2=1,
解得:m=5,或m=3(舍去),
∴点C的坐标为(5,0).
故在x轴上存在点C,使得△ABC为等腰三角形,且AC=AB,点C的坐标为(5,0).
点评 本题考查了反比例函数图象上点的坐标特征、反比例函数的图象、两点间的距离公式以及解无理方程,解题的关键是:(1)利用反比例函数图象上点的坐标特征求出k值;(2)求出两函数另一交点坐标;(3)得出关于m的方程.本题属于中档题,难度不大,解决该题型题目时,联立两函数解析式求出另一交点坐标,根据两函数图象的上下位置关系解出不等式的解集是难点.


科目:初中数学 来源: 题型:解答题
| 分数段(x分) | x≤10 | 11≤x≤15 | 16≤x≤20 | 21≤x≤25 | 26≤x≤30 |
| 人 数 | 10 | 15 | 35 | 112 | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
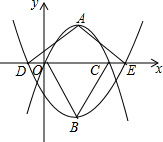 如图,在平面直角坐标系中,抛物线y=a1(x-2)2+2与y=a2(x-2)2-3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1.
如图,在平面直角坐标系中,抛物线y=a1(x-2)2+2与y=a2(x-2)2-3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
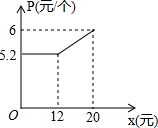 某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.
某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com