
【题目】已知等腰三角形的周长为28cm,其中的一边长是另一边长的![]() 倍,求这个等腰三角形各边的长.
倍,求这个等腰三角形各边的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司,今年三月份与五月份完成投递的快件总件数分别是5万件和![]() 万件,现假定该公司每月投递的快件总件数的增长率相同.
万件,现假定该公司每月投递的快件总件数的增长率相同.
![]() 求该公司投递快件总件数的月平均增长率;
求该公司投递快件总件数的月平均增长率;
![]() 如果平均每人每月可投递快递
如果平均每人每月可投递快递![]() 万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
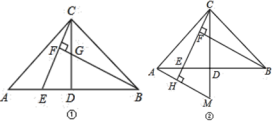
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象过P(1,4),Q(4,1)两点,且与x轴交于A点.
(1)求此一次函数的解析式;
(2)求△POQ的面积;
(3)已知点M在x轴上,若使MP+MQ的值最小,
求点M的坐标及MP+MQ的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
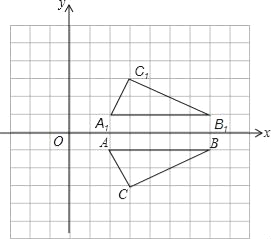
【题目】如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
(1)判定△ABC的形状;
(2)设△ABC关于x轴的对称图形是△A1B1C1,若把△A1B1C1的各顶点的横坐标都加2.纵坐标不变,则△A1B1C1的位置发生什么变化?若最终位置是△A2B2C2,求C2点的坐标;
(3)试问在x轴上是否存在一点P,使PC-PB最大,若存在,求出PC-PB的最大值及P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;(图1)
(2)求∠FAE的度数;(图1)
(3)如图2,延长CF到G点,使BF=GF,连接AG.求证:CD=CG;并猜想CD与2BF+DE的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE. 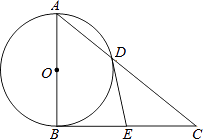
(1)求证:DE与⊙O相切.
(2)若tanC= ![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com