

分析 (1)此类题要充分运用旋转的性质,以及全等三角形的性质得对应角相等,对应边相等,得出∠PAP′=60°,再利用等边三角形的判定得出△APP′为等边三角形,即可得出∠APP′的度数,即可得出答案;
(2)利用已知首先得出△AEG≌△AFE,即可把EF,BE,FC放到一个三角形中,从而根据勾股定理即可证明.
解答 解:(1)将△ABP绕顶点A旋转到△ACP′处,
∴△BAP≌△CAP′,
∴AB=AC,AP=AP′,∠BAP=∠CAP′,
∴∠BAC=∠PAP′=60°,
∴△APP′是等边三角形,
∴∠APP′=60°,
因为B P P′不一定在一条直线上
连接PC,
∴P′C=PB=4,PP′=PA=3,PC=5,
∴∠PP′C=90°,
∴△PP′C是直角三角形,
∴∠APB=∠AP′C=∠APP′+∠P′PC=60°+90°=150°,
∴∠BPA=150°;
故答案是:150°,△ABP;
(2)把△ACF绕点A顺时针旋转90°,得到△ABG.连接EG.
则△ACF≌△ABG.
∴AG=AF,BG=CF,∠ABG=∠ACF=45°.
∵∠BAC=90°,∠GAF=90°.
∴∠GAE=∠EAF=45°,
在△AEG和△AFE中,
∵$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE}\\{AE=AE}\end{array}\right.$
∴△AEG≌△AFE.
∴EF=EG,
又∵∠GBE=90°,
∴BE2+BG2=EG2,
即BE2+CF2=EF2.则三角形是直角三角形.
点评 本题考查了旋转的性质,全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,读懂题目信息,理解利用旋转构造出全等三角形和等边三角形以及直角三角形是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
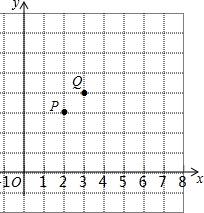 如图,坐标系中有两点P(2,3),Q(3,4).
如图,坐标系中有两点P(2,3),Q(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.
一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com