
【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.
(1)你添加的条件是
(2)在(1)的条件下,不再添加辅助线和字母,证明DE=DF
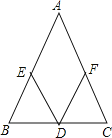
【答案】(1) AB=AC(答案不唯一);(2)证明见解析.
【解析】
(1)答案不唯一,若添加AB=AC,根据AB=AC,推出∠B=∠C,根据ASA证出△BED和△CFD全等即可;或添加∠B=∠C,根据ASA证出△BED和△CFD全等即可;添加∠BED=∠CDF,根据AAS即可推出△BED和△CFD全等;根据∠AED=∠AFD推出∠B=∠C,根据ASA证△BED≌△CFD即可;
(2)根据(1)中添加的条件结合三角形全等的判定方法进行证明即可.
(1)答案不唯一,如AB=AC或∠B=∠C或∠BED=∠CFD,或∠AED=∠AFD等;
(2)①若添加AB=AC,证明如下:
∵AB=AC,
∴∠B=∠C,
在△BED和△CFD中,
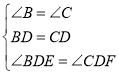 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF;
②若添加∠B=∠C,证明如下:
在△BED和△CFD中,
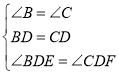 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF;
③若添加∠BED=∠CFD,证明如下:
在△BED和△CFD中,
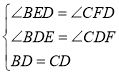 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF;
④若添加∠AED=∠AFD,证明如下:
∵∠AED=∠AFD,∠AED=∠B+∠BDE,∠AFD=∠C+∠CDF,
又∵∠BDE=∠CDF,
∴∠B=∠C,
在△BED和△CFD中,
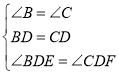 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF.


科目:初中数学 来源: 题型:
【题目】某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
设从甲养殖场调运鸡蛋x斤,总运费为W元
(1)试写出W与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=90°﹣∠BDO.
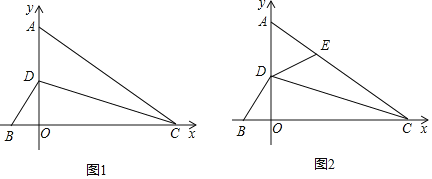
(1)求证:AC=BC;
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5a,AE=a,CF=2a,则BG长是( )

A. ![]() a B.
a B. ![]() a C.
a C. ![]() a D.
a D. ![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD中,E、F分别是BC、DC上的一点,连接AE、AF, AE、AF交于点H且∠AHB=90°.
(1)求证:BE=CF.
(2)若正方形面积是25m2,BE=![]() AD,求AF的长.
AD,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标的原点是等边三角形的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )

A. (0,1) B. (﹣![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在A1处,已知OA=![]() ,AB=1,则点A1的坐标是( )
,AB=1,则点A1的坐标是( )

A. (![]() ) B. (
) B. (![]() ) C. (
) C. (![]() ) D. (
) D. (![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .
.
(1)根据要求作图:在边![]() 上求作一点
上求作一点![]() ,使得点
,使得点![]() 到
到![]() 、
、![]() 的距离相等,在边
的距离相等,在边![]() 上求作一点
上求作一点![]() ,使得点
,使得点![]() 到点
到点![]() 、
、![]() 的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
的距离相等;(不需要写作法,但需要保留作图痕迹和结论)
(2)在第(1)小题所作出的图中,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com