

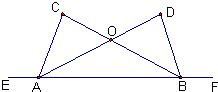
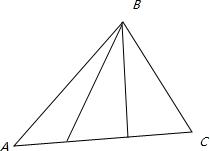
 解:
解: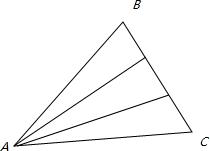 ;
;

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:浙江省期末题 题型:解答题
| 附加题:某市对电话费作了调整,原市话费为:每3分钟0.2元(不足3分钟按3分钟计算);现在调整为:前3分钟为0.2元,以后每分钟加收0.1元(不足1分钟按1分钟计算).设通话时间x分钟时,调整前的话费为a元,调整后的话费为b元. ①填写下表:  ②指出x取何值时,a不超过b; ③当x=11时,请你按调整后的收费方法设计三种通话方案(可以分几次拨打),使所需话费c满足关系式:c<b. |
查看答案和解析>>
科目:初中数学 来源:黄冈 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《二元一次方程组》(02)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com