
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
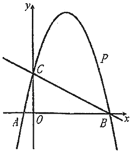
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,设点
上方抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①求![]() 面积最大值和此时
面积最大值和此时![]() 的值;
的值;
②![]() 是直线
是直线![]() 上一动点,是否存在点
上一动点,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,直接写出点
为顶点的四边形是平行四边形,若存在,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①当
;(2)①当![]() 时
时![]() ,②
,②![]()
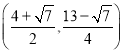 ,
,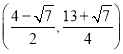
【解析】
(1)求出点B、C的坐标,将点B、C的坐标代入抛物线表达式,即可求解;
(2)①过点P作y轴的平行线交直线BC于点H,根据△PBC面积=![]() ×PH×OB,利用二次函数的性质即可求解;②分AB是平行四边形的边,AB是平行四边形的对角线两种情况,分别求解即可.
×PH×OB,利用二次函数的性质即可求解;②分AB是平行四边形的边,AB是平行四边形的对角线两种情况,分别求解即可.
解:(1)∵直线![]() 经过点B,C,
经过点B,C,
∴点B、C的坐标分别为:(4,0)、(0,2),
将点B、C的坐标代入抛物线表达式,得![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为:![]() ;
;
(2)①过点P作y轴的平行线交直线BC于点H,
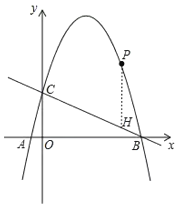
则点P(m,![]() ),点H(m,
),点H(m,![]() ),
),
∴△PBC面积=![]() ×PH×OB=
×PH×OB=![]() ×4×(
×4×(![]() )=2m2+8m=2(m-2)2+8,
)=2m2+8m=2(m-2)2+8,
∴当m=2时,面积存在最大值8;
②设点P(m,![]() ),点Q(n,
),点Q(n,![]() ),
),
令 ∴点A的坐标为:( 当AB是平行四边形的边时,点A向右平移 同样点P(Q)向右平移 则m± 解得:m= ∴此时P点坐标为 当AB是平行四边形的对角线时, 由中点公式得:m+n= 解得:m= 综上点P的坐标为:![]() ,解得:
,解得: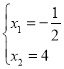 ,
,![]() ,0),
,0),![]() 个单位得到B,
个单位得到B,![]() 个单位得到Q(P),
个单位得到Q(P),![]() =n,
=n,![]() =
=![]() ,
,![]() (舍去)或
(舍去)或![]() (舍去)或
(舍去)或![]() ,
,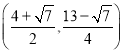 或
或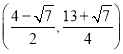 ;
;![]() ,
,![]() ,
,![]() 或
或![]() (重复,舍去);
(重复,舍去);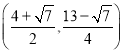 或
或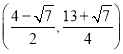 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
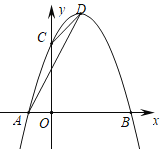
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点,分别连接AC、CD、AD.
(1)求抛物线的函数解析式以及顶点D的坐标;
(2)在抛物线上取一点P(不与点C重合)、并分别连接PA、PD,当△PAD的面积与△ACD的面积相等时,求点P的坐标:
查看答案和解析>>
科目:初中数学 来源: 题型:
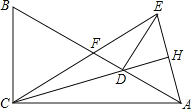
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=![]() +
+![]() ,点D为边AB上一点,连接CD.将△ACD沿直线CD翻折至△ECD,CE恰好过AB的中点F.连接AE交CD的延长线于点H,若∠ACD=15°,则DH的长为( )
,点D为边AB上一点,连接CD.将△ACD沿直线CD翻折至△ECD,CE恰好过AB的中点F.连接AE交CD的延长线于点H,若∠ACD=15°,则DH的长为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
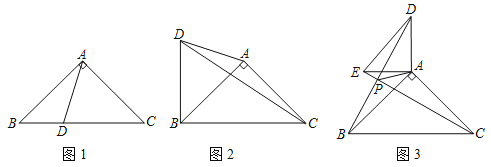
【题目】在△ABC中,AB=AC,∠BAC=90°,D为平面内的一点.
(1)如图1,当点D在边BC上时,且∠BAD=30°,求证:AD=![]() BD.
BD.
(2)如图2,当点D在△ABC的外部,且满足∠BDC﹣∠ADC=45°,求证:BD=![]() AD.
AD.
(3)如图3,若AB=4,当D、E分别为AB、AC的中点,把△DAE绕A点顺时针旋转,设旋转角为α(0<α≤180°),直线BD与CE的交点为P,连接PA,直接写出△PAC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图:

请你根据以上的信息,回答下列问题:
(1) 本次共调查了_____名学生,其中最喜爱戏曲的有_____人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是______;
(2) 根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.
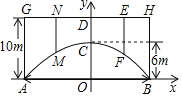
(1)以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;
(2)若支柱每米造价为2万元,求5根支柱的总造价;
(3)拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
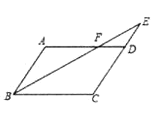
【题目】如图,在口ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= ![]() CD
CD
(1)求证:△ABF∽△CEB
(2)若△DEF的面积为2,求△CEB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有![]() 个标号分别为
个标号分别为![]() 的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为
的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为![]() ,再从剩下的
,再从剩下的![]() 个小球中随机取出一个小球,记下标号为
个小球中随机取出一个小球,记下标号为![]() 记点
记点![]() 的坐标为
的坐标为![]() .
.
(1)请用画树形图或列表的方法写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求两次取出的小球标号之和大于![]() 的概率;
的概率;
(3)求点![]() 落在直线
落在直线![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com