
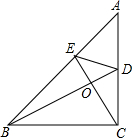
 如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:
如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:
|
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
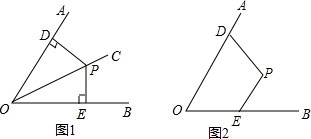
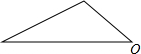 在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90°,180°,270°得到的图形组成的,请你画出这个图案,并描述这个图案像什么.
在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90°,180°,270°得到的图形组成的,请你画出这个图案,并描述这个图案像什么.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com