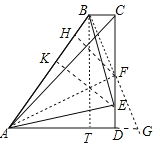
【题目】如图四边形ABCD中，AD∥BC，∠BCD=90°，AB=BC+AD，∠DAC=45°，E为CD上一点，且∠BAE=45°．若CD=4，则△ABE的面积为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】解：如图取CD的中点F，连接BF延长BF交AD的延长线于G，作FH⊥AB于H，EK⊥AB于K．作BT⊥AD于T．∵BC∥AG，∴∠BCF=∠FDG，∵∠BFC=∠DFG，FC=DF，∴△BCF≌△GDF，∴BC=DG，BF=FG，∵AB=BC+AD，AG=AD+DG=AD+BC，∴AB=AG，∵BF=FG，∴BF⊥BG，∠ABF=∠G=∠CBF，∵FH⊥BA，FC⊥BC，∴FH=FC，易证△FBC≌△FBH，△FAH≌△FAD，∴BC=BH，AD=AB，由题意AD=DC=4，设BC=TD=BH=x，在Rt△ABT中，∵AB2=BT2+AT2，∴（x+4）2=42+（4﹣x）2，∴x=1，∴BC=BH=TD=1，AB=5，设AK=EK=y，DE=z，∵AE2=AK2+EK2=AD2+DE2，BE2=BK2+KE2=BC2+EC2，∴42+z2=y2①，（5﹣y）2+y2=12+（4﹣z）2②，由①②可得y=
，∴S△ABE=
×5×
=
，故选D．
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案科目：初中数学 来源： 题型：
【题目】如图，直线AE与CD相交于点B，射线BF平分∠ABC，射线BG在∠ABD内，
（1）若∠DBE的补角是它的余角的3倍，求∠DBE的度数；
（2）在（1）的件下，若∠DBG=∠ABG﹣33°，求∠ABG的度数；
（3）若∠FBG=100°，求∠ABG和∠DBG的度数的差．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点P的坐标为(a﹣1，5﹣2a)，且它到两个坐标轴的距离相等，则点P的坐标为( )
A.(3，3)B.(3，﹣3)C.(1，﹣1)D.(1，1)或(3，﹣3)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A，B两城相距300千米；
②乙车比甲车晚出发1小时，却早到1小时；
③乙车出发后2.5小时追上甲车；
④当甲、乙两车相距50千米时，t=
或
．
其中正确的结论有（ ）
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：线段
、
、
；
求作：△ABC，使
， 
， 
；
【答案】答案见解析
【解析】试题分析：先画出与
相等的角，再画出
的长，连接
，则
即为所求三角形．
试题解析：如图所示：①先画射线BC，
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′；
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧，交于点E；
④在BF上取点C，使CB=a，以B为圆心，c为半径画圆交BE的延长线于点A，连接AC，
结论：△ABC即为所求三角形.
【题型】解答题
【结束】
15
【题目】已知：线段
， 
，求作： 
，使
， 
．
查看答案和解析>>
科目：初中数学 来源： 题型：
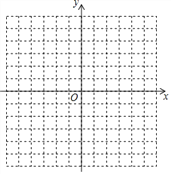
【题目】（1）在如图所示的平面直角坐标系中表示下面各点：A（0，3）；B（5，0）；C（3，-5）；D（-3，-5）；E（3，5）；
（2）连接CE，则直线CE与y轴是什么位置关系？
（3）点D分别到x、y轴的距离是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，我们定义直线y=ax﹣a为抛物线
（a、b、c为常数，a≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．
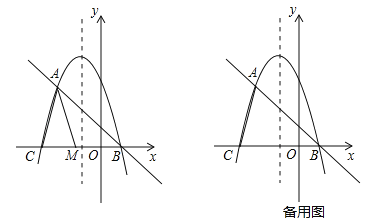
已知抛物线
与其“梦想直线”交于A、B两点（点A在点B的左侧），与x轴负半轴交于点C．
（1）填空：该抛物线的“梦想直线”的解析式为 ，点A的坐标为 ，点B的坐标为 ；
（2）如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；
（3）当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F，使得以点A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点E、F的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com