
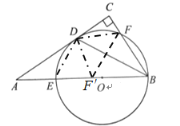
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,在
,在![]() 上取点
上取点![]() ,以点
,以点![]() 为圆心经过
为圆心经过![]() 、
、![]() 两点画圆分别与
两点画圆分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() (异于点
(异于点![]() ).
).
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 恰好是
恰好是![]() 的中点,求
的中点,求![]() 的长;
的长;
(3)若![]() 的长为
的长为![]() .
.
①求![]() 的半径长;
的半径长;
②点![]() 关于
关于![]() 轴对称后得到点
轴对称后得到点![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
【答案】(1)见解析;(2)![]() ;(3)①
;(3)①![]() 或
或![]() ;②
;②![]() 或
或![]()
【解析】
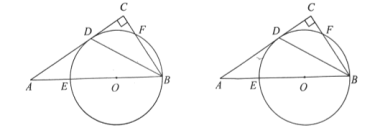
(1)连接DO,如图,先根据角平分线的定义以及平行线的性质,得出∠1=∠3,从而得到DO∥BC,再根据∠C=90°,可得出结果;
(2)连接FO,根据E为中点,可以得出![]() ,在Rt△AOD中,可以求出sinA的值,从而得出∠A的度数,再证明△BOF为等边三角形,从而得出∠BOF的度数,根据弧长公式可得出结果;
,在Rt△AOD中,可以求出sinA的值,从而得出∠A的度数,再证明△BOF为等边三角形,从而得出∠BOF的度数,根据弧长公式可得出结果;
(3)①设圆的半径为r,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,四边形
,四边形![]() 是矩形.再证明
是矩形.再证明![]() ,得出
,得出![]() ,据此列方程求解;
,据此列方程求解;
②作出点F关于BD的对称点F′,连接DE,DF,DF′,FF′,再证明![]() ,最后根据相似三角形的面积比等于相似比的平方求解.
,最后根据相似三角形的面积比等于相似比的平方求解.
(1)证明:连结![]() ,
,

∵![]() 平分
平分![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .∴
.∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() 是
是![]() 的切线.
的切线.
(2)解:∵![]() 是
是![]() 中点,∴
中点,∴![]() .
.
∴![]() ,∴
,∴![]() ,
,![]() .
.
连接FO,
又BO=OF,∴△BOF为等边三角形,
∴![]() .
.
∴![]() .
.
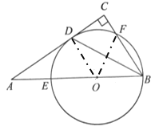
(3)解:①过![]() 作
作![]() 于
于![]() ,则
,则![]() ,四边形
,四边形![]() 是矩形.
是矩形.
设圆的半径为![]() ,则
,则![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
而![]() ,∴
,∴![]() .
.
∴![]() 即
即 ,
,
解之得![]() ,
,![]() .
.

②作出点F关于BD的对称点F′,连接FF′,DE,DF,DF′,
∵∠EBD=∠FBD,∴![]() .
.
∵![]() 是直径,∴
是直径,∴![]() ,
,
而![]() 、
、![]() 关于
关于![]() 轴对称,∴
轴对称,∴![]() ,
,![]() ,DF=DF′,
,DF=DF′,
∴DE∥FF′,DE=DF′,∠DEF′=∠DF′E,
∴![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
由①知![]() ,而
,而![]() ,
,
∴![]() .
.
又易得△BCD∽△BDE,∴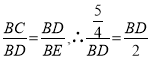 ,∴BD2=
,∴BD2=![]() .
.
在Rt△BED中,DE2=BE2-BD2=4-![]() =
=![]() ,∴DE=
,∴DE=![]() =DF′.
=DF′.
∴![]() 与
与![]() 的面积比
的面积比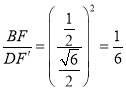 .
.
同理可得,当![]() 时,
时,![]() 与
与![]() 的面积比
的面积比![]() .
.
∴![]() 与
与![]() 的面积比为
的面积比为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与探究:
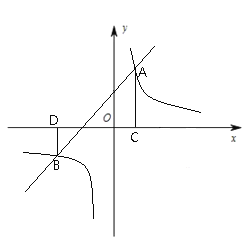
如图所示,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
(1)求![]() ,
,![]() 的值及反比例函数的函数表达式;
的值及反比例函数的函数表达式;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请求出此时点
,请求出此时点![]() 的坐标;
的坐标;
(3)小颖在探索中发现:在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形.请你直接写出点
为顶角的等腰三角形.请你直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图像与边长是6的正方形
的图像与边长是6的正方形![]() 的两边
的两边![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)若点![]() 是
是![]() 边的中点,求反比例函数
边的中点,求反比例函数![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式及
的解析式及![]() 的面积
的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
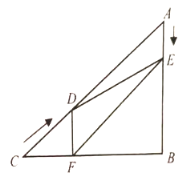
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,动点
;同时,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停止运动.设点
;当一个点停止运动,另一个点也停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]()
![]()
![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球,它们分别标有数字0,1,2,3,小明从布袋里随机摸出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机摸出一个小球,记下数字为
,小红在剩下的3个小球中随机摸出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)画树状图或列表,写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若![]() 在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
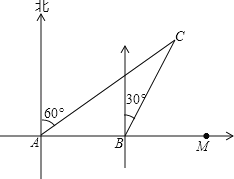
【题目】如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,
(1)求B到C的距离;
(2)如果在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由(![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农科院新培育岀A、B两种新麦种,为了了解它们的发芽情况,在推广前做了五次发芽实验,每次随机各自取相同种子数,在相同的培育环境中分别实验,实验情况记录如下:
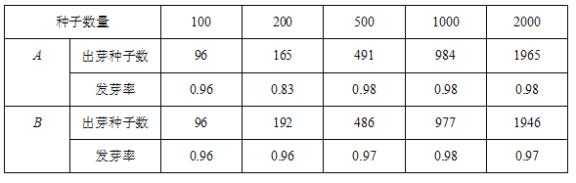
下面有三个推断:
①在同样的地质环境下播种,A种子的出芽率可能会高于B种子.
②当实验种子数里为100时,两种种子的发芽率均为0.96所以他发芽的概率一样;
③随着实验种子数量的增加,A种子出芽率在0.98附近摆动,显示出一定的稳定性,可以估计A种子出芽的概率是0.98;其中不合理的是_____(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
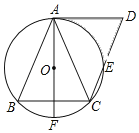
【题目】如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
(1)求证:AD是⊙O的切线;
(2)若∠BAC=45°,AF=2,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com