
分析 设c=5k,a=3k,由勾股定理可求得b=4k,可求得tanA=$\frac{3}{4}$,接下来利用三角形的周长为48可求得两直角边的长,最后即可求得△ABC的面积.
解答 解:设c=5k,a=3k.
由勾股定理得:b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{(5k)^{2}-(3k)^{2}}$=4k.
∴tanA=$\frac{3k}{4k}$=$\frac{3}{4}$.
∵△ABC的周长为48,
∴5k+3k+4k=48.
解得:k=4.
∴3k=3×4=12,4k=4×4=16.
∴△ABC的面积=$\frac{1}{2}×12×16$=96.
故答案为:$\frac{3}{4}$;96.
点评 本题主要考查的是锐角函数值的定义、勾股定理的应用,求得a、b、c的长度是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在班上组织的“元旦迎新晚会”中,小丽和小芳都想当节目主持人,但现在只有一个名额.小芳想出了一个用游戏来选人的办法,她将一个转盘平均分成6份,如图所示.游戏规定:随意转动转盘,若指针指到偶数,则小丽去;若指针指到奇数,则小芳去.(1)指针指到偶数的概率是多少?指针指到奇数的概率是多少?
在班上组织的“元旦迎新晚会”中,小丽和小芳都想当节目主持人,但现在只有一个名额.小芳想出了一个用游戏来选人的办法,她将一个转盘平均分成6份,如图所示.游戏规定:随意转动转盘,若指针指到偶数,则小丽去;若指针指到奇数,则小芳去.(1)指针指到偶数的概率是多少?指针指到奇数的概率是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
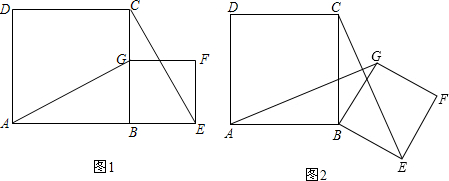
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
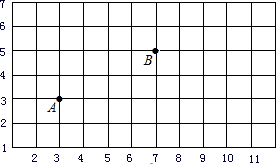 如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.
如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com