练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．下列两个条件：①y随x的增大而减小；②图象经过点（1，2）．写出1个同时具备条件①、②的一个一次函数表达式y=-x+3．

    分析 根据①得k＜0，写出一个数即可，再根据②，把（1，2）代入一次函数的解析式y=kx+b得出解析式即可．

    解答 解：∵y随x的增大而减小，
    ∴取k=-1，
    ∵图象经过点（1，2），
    ∴设解析式为y=kx+b，
    即-1+b=2，
    解得b=3，
    ∴同时具备条件①、②的一个一次函数表达式为y=-x+3，
    故答案为y=-x+3．

    点评 本题考查了一次函数的性质，是一道开放性的题目，一次函数中当k＞0时，y随x的增大而增大，k＜0时，y随x的怎大而减小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．解下列方程
    （1）x2-4x+2=0
    （2）2x2-4x=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．2014年底我县人口约370000人，将370000用科学记数法表示为3.7×105．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．为制定本市初中七、八、九年级学生的校服的生产计划，有关部门准备对180名初中男生的身高作调查，现有三种调查方案：A．测量少年体校中180名男子篮球、排球队员的身高；B．查阅有关外地180名男生身高的统计资料；C．在本市的市区和郊县各任选一所完全中学、两所初级中学，在这六所学校的有关年级的（1）班中，用抽签的方法分别选出10名男生，然后测量他们的身高．
    （1）为了达到估计本市初中这三个年级男生身高的目的，你认为采用上述哪一种调查方案比较合理，为什么？
    答：选C；理由这样获得的数据有代表性．
    （2）下表中的数据是使用了某种调查方案获得的：
    ①根据表中的数据填写表中的空格；           
    ②根据填写的数据补全频数分布直方图．
    初中男生身高情况抽样调查表
    人数
    身高（cm）    		总计（频数）总计（频数）
    143～1539 0.05
    153～16327 0.15
    163～173810.45
    173～183450.25
    183～193180.01
    （注：每组可含最低值，不含最高值）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算
    （1）$\sqrt{18}+\sqrt{27}÷{（\sqrt{3}）^2}-\sqrt{8}$．
    （2）${（\sqrt{2}+1）^2}+\frac{1}{{\sqrt{3}-\sqrt{2}}}-（\sqrt{5}+\sqrt{3}）（\sqrt{5}-\sqrt{3}）-|1-\sqrt{2}|$．
    （3）$4×{2^{-2}}+{（\sqrt{5}-1）^0}-|-2|+\sqrt{2}×\sqrt{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．计算1-3等于（　　）
    A．2B．-2C．-$\frac{1}{3}$D．$-\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．若x2+2x的值是3，则2-x2-2x的值是-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．找出以如图形变化的规律，则第20个图形中黑色正方形的数量是（　　）
    A．28B．29C．30D．31

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

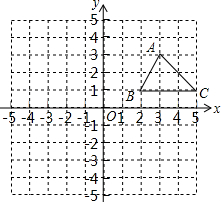    5．如图，△ABC的三个顶点在平面直角坐标系中的坐标分别为A（3，3），B（2，1），C（5，1），将△ABC绕点O逆时针旋转180°得△A′B′C′，请你在平面直角坐标系中画出△A′B′C′，并写出△A′B′C′的顶点坐标．

    查看答案和解析>>

    同步练习册答案