
【题目】如图1,AD∥BC,AB ⊥BC于B,∠DCB=75°,以CD为边的等边△DCE的另一顶点E在线段AB上.
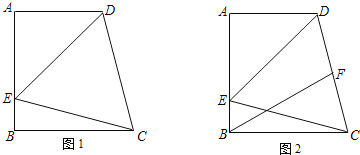
(1)填空:∠ADE=____°;
(2)求证: AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,求![]() 的值.
的值.
【答案】(1)45;(2)证明见解析(3)1.
【解析】
解:(1)∵∠DCB=75°,AD∥BC,
∴∠ADC=105°
∵△DCE为等边三角形,
∴∠EDC=60°,
∴∠ADE=∠ADC-∠EDC=45°.
(2)证明:连接AC
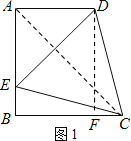
由(1)知∠ADE =45,
∵AB⊥BC,AD∥BC,
∴∠DAB=90 ,
∴∠AED=45,
∴AD=AE,
∴点A在线段DE的垂直平分线上,
∵△DCE为等边三角形,
∴CD=CE,
∴点C也在线段DE的垂直平分线上 ,
∴AC就是线段DE的垂直平分线,
即AC⊥DE,
∴AC平分∠EAD,
∴∠BAC=45°,
∴△ABC是等腰直角三角形
∴BA=BC
(3)解:连接AF,延长BF交AD的延长线于点G
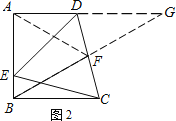
∵∠FBC=30,∠ABC=90,
∴∠ABF=60,
∵∠DCB=75,
∴∠BFC=75,
故BC=BF,
由(2)知:BA=BC,
∴BA=BF,
∴△ABF是等边三角形,
∴AB=BF=FA,
∴∠BAC=60 ,
∴∠DAF=30,
又∵AD∥BC,
∴∠FAG=∠G=30,
∴FG =FA= FB,
又∠DFG=∠CFB,
∴△BCF≌△GDF(ASA),
∴DF=CF,
∴![]() =1.
=1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今年考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是 ,破译“正做数学”的真实意思是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.

请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c–3b<0;⑤a+b>n(an+b)(n≠1),其中正确的结论有( )
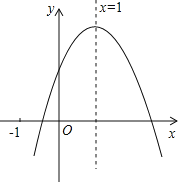
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
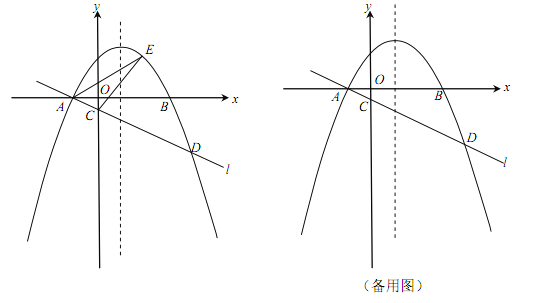
【题目】(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线![]() (
(![]() )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:![]() 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com