
【题目】如图,把等边三角形![]() 沿着
沿着![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,且
处,且![]() 。若
。若![]() ,
,![]() ,则
,则![]() ______
______![]() .(在直角三角形中,
.(在直角三角形中,![]() 角所对的直角边等于斜边的一半。)
角所对的直角边等于斜边的一半。)

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=6,则S1+S5=_____.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
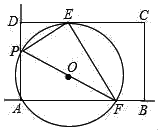
【题目】如图,矩形ABCD中,AD=10,CD=15,E是边CD上一点,且DE=5,P是射线AD上一动点,过A,P,E三点的⊙O交直线AB于点F,连结PE,EF,PF,设AP=m.
(1)当m=6时,求AF的长.
(2)在点P的整个运动过程中.
①tan∠PFE的值是否改变?若不变,求出它的值;若改变,求出它的变化范围.
②当矩形ABCD恰好有2个顶点落在⊙O上时,求m的值.
(3)若点A,H关于点O成中心对称,连结EH,CH.当△CEH是等腰三角形时,求出所有符合条件的m的值.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
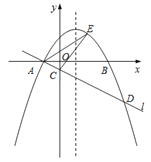
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,且
,且![]() .
.
![]() 直接写出点
直接写出点![]() 的坐标,并求直线
的坐标,并求直线![]() 的函数表达式(其中
的函数表达式(其中![]() ,
,![]() 用含
用含![]() 的式子表示);
的式子表示);
![]() 点
点![]() 是直线
是直线![]() 上方的抛物线上的一点,若
上方的抛物线上的一点,若![]() 的面积的最大值为
的面积的最大值为![]() ,求
,求![]() 的值;
的值;
![]() 设
设![]() 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点![]() 在抛物线上,以点
在抛物线上,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,如取款、上网等都需要密码,有一种利用“因式分解”产生的密码,方便记忆,原理是:如多项式![]() ,若
,若![]() ,
,![]() 时,则各因式的值为
时,则各因式的值为![]() ,
,![]() ,
,![]() ,于是把018162作为一个六位数的密码,对于多项式
,于是把018162作为一个六位数的密码,对于多项式![]() ,取
,取![]() ,
,![]() 时,用上述方法产生的密码是_________________.(写一个即可)
时,用上述方法产生的密码是_________________.(写一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=2S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )

A. ①②③ B. ②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
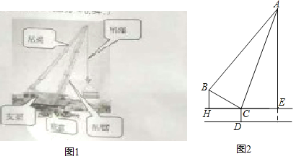
【题目】如图分别是吊车在吊一物品时的实物图与示意图.已知吊车底盘![]() 的高度为
的高度为![]() 米,支架
米,支架![]() 的长为
的长为![]() 米,且与地面成
米,且与地面成![]() 角,吊绳
角,吊绳![]() 与支架
与支架![]() 的夹角为
的夹角为![]() ,吊臂
,吊臂![]() 与地面成
与地面成![]() 角.(参考数据:
角.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
![]() 求吊绳与吊臂的长度.
求吊绳与吊臂的长度.
![]() 求吊车的吊臂顶端
求吊车的吊臂顶端![]() 点距地面的高度是多少米.(精确到
点距地面的高度是多少米.(精确到![]() 米)
米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com