
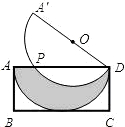
 如图在矩形ABCD中,AB=1,AD=2,现将一块直径为2的半圆形纸片放置在矩形ABCD中,使其直径与AD重合,若将半圆上点D固定,再把半圆往矩形外旋至A′D处,半圆弧A′D与AD交于点P,设∠ADA′=α.
如图在矩形ABCD中,AB=1,AD=2,现将一块直径为2的半圆形纸片放置在矩形ABCD中,使其直径与AD重合,若将半圆上点D固定,再把半圆往矩形外旋至A′D处,半圆弧A′D与AD交于点P,设∠ADA′=α.| 2 |
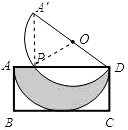 解:(1)连接PA′,
解:(1)连接PA′,| 2 |
| 2 |
| DP |
| DA′ |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 120π |
| 360 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| ||
| 4 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
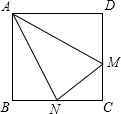 如图在矩形ABCD中,M为CD上一点,沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,∠DAM=30°,则AN=
如图在矩形ABCD中,M为CD上一点,沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,∠DAM=30°,则AN=查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏南京市玄武区九年级第一学期期末考试数学试卷(解析版) 题型:解答题
如图,在矩形ABCD中,点O是边AD上的中点,点E是边BC上的一个动点,延长EO到F,使得OE=OF.

(1)当点E运动到什么位置时,四边形AEDF是菱形?(直接写出答案)
(2)若矩形ABCD的周长为20,四边形AEDF的面积是否存在最大值?如果存在,请求出最大值;如果不存在,请说明理由.
(3)若AB= ,BC=
,BC=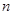 ,当
,当 .
.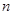 满足什么条件时,四边形AEDF能成为一个矩形?(不必说明理由)
满足什么条件时,四边形AEDF能成为一个矩形?(不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com