
分析 ①正确.画出函数图象即可判断.
②错误.由图象可知,-$\frac{b}{2a}$>-$\frac{1}{2}$,推出b>a,故b-a可以是正数,所以a+3b+2c=a+3b-2a-2b=b-a>0,故错误.
③正确.利用函数y1=$\frac{a}{b}$x2+x=$\frac{a}{b}$(x2+$\frac{b}{a}$x)=$\frac{a}{b}$(x+$\frac{b}{2a}$)2-$\frac{b}{4a}$,根据函数的最值问题即可解决.
④令y=0则ax2+bx-a-b=0,设它的两个根为x1,1,则x1•1=$\frac{-a-b}{a}$=-$\frac{a+b}{a}$,求出x1即可解决问题.
解答 解:由题意二次函数图象如图所示,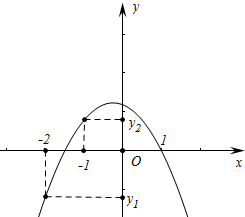
∴a<0.b<0,c>0,
∴abc>0,故①正确.
∵-$\frac{b}{2a}$>-$\frac{1}{2}$,
∵a<0,
∴b>a,
∴b-a>0,
∵a+b+c=0,
∴c=-a-b,
∴a+3b+2c=a+3b-2a-2b=b-a>0,
∴a+3b+2c≤0,故②错误.
∵函数y1=$\frac{a}{b}$x2+x=$\frac{a}{b}$(x2+$\frac{b}{a}$x)=$\frac{a}{b}$(x+$\frac{b}{2a}$)2-$\frac{b}{4a}$,
∵$\frac{a}{b}$>0,
∴函数y1有最小值-$\frac{b}{4a}$,
∴$\frac{a}{b}$x2+x≥-$\frac{b}{4a}$,故③正确.
∵y=ax2+bx+c的图象经过点(1,0),
∴a+b+c=0,
∴c=-a-b,
令y=0则ax2+bx-a-b=0,设它的两个根为x1,1,
∵x1•1=$\frac{-a-b}{a}$=-$\frac{a+b}{a}$,
∴x1=-$\frac{a+b}{a}$,
∵-2<x1<x2,
∴在-2<x<-1中存在一个实数x0,使得x0=-$\frac{a+b}{a}$,故④正确,
故答案为②.
点评 本题考查二次函数的图象与系数的关系、二次函数图象上的点的坐标特征,解题的关键是灵活应用二次函数的性质解决问题,学会构建二次函数解决最值问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=x2+bx+c图象顶点为C,与直线y=x+m图象交于AB两点,其中A点的坐标为(3,4),B点在y轴上.
如图,已知二次函数y=x2+bx+c图象顶点为C,与直线y=x+m图象交于AB两点,其中A点的坐标为(3,4),B点在y轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为( )
我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为( )| A. | 5.5×106千米 | B. | 5.5×107千米 | C. | 55×106千米 | D. | 0.55×108千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 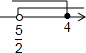 | B. | 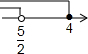 | C. | 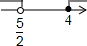 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必然事件发生的概率等于0.5 | |
| B. | 5名同学二模的数学成绩是92,95,95,98,110,则他们的平均分是98分,众数是95 | |
| C. | 射击运动员甲、乙分别射击10次且击中环数的方差分别是5和18,则乙较甲稳定 | |
| D. | 要了解金牌获得者的兴奋剂使用情况,可采用抽样调查的方法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com