
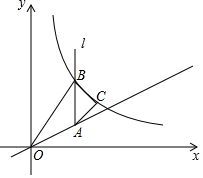
 如图,已知点A是一次函数y=$\frac{1}{2}$x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=$\frac{k}{x}$(x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是3.
如图,已知点A是一次函数y=$\frac{1}{2}$x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=$\frac{k}{x}$(x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是3. 分析 作辅助线,构建直角三角形,设AB=2a,根据直角三角形斜边中线是斜边一半得:BE=AE=CE=a,设A(x,$\frac{1}{2}$x),则B(x,$\frac{k}{x}$),C(x+a,$\frac{k}{x+a}$),因为B、C都在反比例函数的图象上,列方程组可得结论.
解答 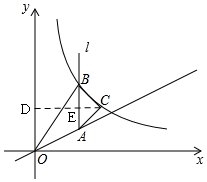 解:如图,过C作CD⊥y轴于D,交AB于E,
解:如图,过C作CD⊥y轴于D,交AB于E,
∵AB⊥x轴,
∴CD⊥AB,
∵△ABC是等腰直角三角形,
∴BE=AE=CE,
设AB=2a,则BE=AE=CE=a,
设A(x,$\frac{1}{2}$x),则B(x,$\frac{k}{x}$),C(x+a,$\frac{k}{x+a}$),
∴$\left\{\begin{array}{l}{{S}_{△OAB}=\frac{1}{2}AB•DE=\frac{1}{2}•2a•x=6①}\\{\frac{k}{x}=2a+\frac{1}{2}x②}\\{\frac{k}{a+x}=a+\frac{1}{2}x③}\\{\;}\end{array}\right.$,
由①得:ax=6,
由②得:2k=4ax+x2,
由③得:2k=2a(a+x)+x(a+x),
2a2+2ax+ax+x2=4ax+x2,
2a2=ax=6,
a2=3,
∵S△ABC=$\frac{1}{2}$AB•CE=$\frac{1}{2}$•2a•a=a2=3.
故答案为:3.
点评 本题考查了反比例函数图象上点的坐标特征、等腰直角三角形的性质、三角形面积,熟练掌握反比例函数上的点符合反比例函数的关系式是关键.


科目:初中数学 来源: 题型:选择题
| A. | 对角线相等四边形是矩形 | |
| B. | 对角线相互垂直平分四边形是菱形 | |
| C. | 对角线相互垂直且相等的平行四边形是正方形 | |
| D. | 对角线相互平分的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解全省中学生的课外阅读情况,选择全面调查 | |
| B. | 为了解某一品牌家具的甲醛含量,选择抽样调查 | |
| C. | 为了解一批袋装食品是否含有防腐剂,选择全面调查 | |
| D. | 某企业招聘员工,对应聘人员进行面试,选择抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1是1的平方根 | |
| B. | 若a>b,c为任意实数,则ac>bc | |
| C. | 无理数可分类为:正无理数、零、负无理数 | |
| D. | 把方程3x-2y=-1改写成用含x的式子表示y的形式是y=$\frac{3}{2}x-\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com