
分析 (1)根据总利润=A种产品的利润+B种产品的利润即可计算.
(2)列出不等式组即可解决问题.
(3)利用一次函数的增减性,即可解决问题.
解答 解:(1)∵A种产品的生产件数是x,B种产品的生产件数是(50-x),
由题意:y=700x+1200(50-x)=-500x+60000.
(2)由题意:$\left\{\begin{array}{l}{9x+4(50-x)≤360}\\{3x+10(50-x)≤290}\end{array}\right.$解得30≤x≤32,
∵x为众数,
∴x=30,31,32.
∴生产方案有3种:
方案1:A种产品:30件,B种产品20件.
方案2:A种产品:31件,B种产品19件.
方案3:A种产品:32件,B种产品18件.
(3)在y=-500x+60000中,
∵-500<0,
∴y随x增加而减小,
∴x=30时,y有最大值=-500×30+60000=45000元.
点评 本题考查一次函数的应用,一元一次不等式组等知识,解题的关键是理解题意,学会利用不等式解决实际问题,学会利用一次函数的增减性解决最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
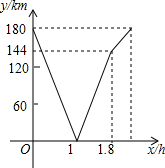 一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.
一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
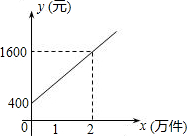 某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com