
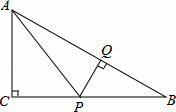
��Rt��ABC�У���C=90�㣬P��BC���ϲ�ͬ��B��C��һ���㣬��P��PQ��AB������ΪQ������AP��
��1����˵�����۵�P��BC���Ϻδ�ʱ�����С�PBQ���ABC���ƣ�
��2����AC=3��BC=4����BPΪ��ֵʱ����AQP������������ֵ��
��3����Rt��ABC�У�����ֱ�DZ�BC��AC�����ϵʽBC=��AC���Ƿ����һ���˵�ֵ��ʹRt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�
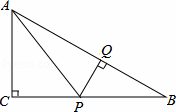


�⣺��1�����۵�P��BC���Ϻδ�ʱ������
��PQB=��C=90�㣬��B=��B
���PBQ�ס�ABC��
��2����BP=x��0��x��4�����ɹ��ɶ������� AB=5
���ɣ�1��֪����PBQ�ס�ABC��
��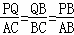 ����
���� 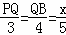
��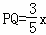
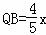
S��APQ=
=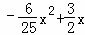
=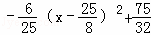
�൱ ʱ����APQ�����������ֵ��
ʱ����APQ�����������ֵ��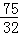 ��
��
��3�����ڣ�
��Rt��AQP��Rt��ACP
��AQ=AC
��Rt��AQP��Rt��BQP
��AQ=QB
��AQ=QB=AC
��Rt��ABC�У��ɹ��ɶ����� BC2=AB2��AC2
��BC=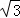 AC
AC
���=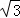 ʱ��Rt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�
ʱ��Rt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
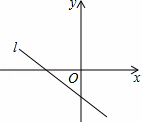
��ͼ��ֱ��l�����ڶ������������ޣ�l�Ľ���ʽ��y=��m��2��x+n����m��ȡֵ��Χ�������ϱ�ʾΪ��������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��װ������ij���װ��һ����װ�ı��Ϊ300Ԫ��������۵İ������ۣ��Կɻ���20%��������װÿ���Ľ���������Ԫ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
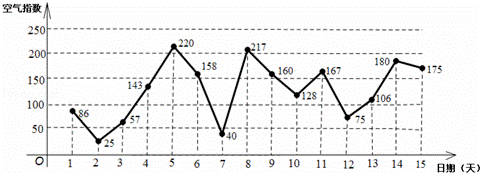
��ͼ��������6��1����15�յĿ�������ָ����������ͳ��ͼ����������ָ��С��100��ʾ����������������������ָ������200��ʾ���������ض���Ⱦ��ij�����ѡ��6��1����6��14���е�ijһ�쵽����������ͣ��2�죮
��1������˵��ﵱ���������������������
��2�������������ͣ��2���ڼ�ֻ��һ������������ض���Ⱦ�ĸ��ʣ�
��3��������ͳ��ͼ�жϴ����쿪ʼ��������Ŀ�������ָ���������ֻд���ۣ���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���㣨��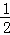 xy2��3�������ȷ���ǣ�������
xy2��3�������ȷ���ǣ�������
�� A�� 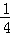 x2y4 B�� ��
x2y4 B�� ��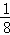 x3y6 C��
x3y6 C�� 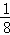 x3y6 D�� ��
x3y6 D�� ��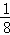 x3y5
x3y5


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�����ݣ�-2��1��1��0��2��1�����������ݵ������ǣ� ��
A��-2 B��0 C��1 D��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������������y=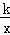 ��kΪ��������k��0��������A��1��3����
��k��������k��0��������A��1��3����
��1�����������Ľ���ʽ��
��2����x������������һ��B������AOB�����Ϊ6����ֱ��AB�Ľ���ʽ��



�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com