如图1.在△ABC中.AB=5.BC=6.AC=4.点D从A出发.在AB边上以每秒1个单位的速度向B运动.过点D作DE∥BC交AC于E.过点D作DF∥AC交BC于F.运动时间为t秒．(1)当t为何值时.四边形DFCE为菱形,(2)如图2.G为边BC上任一点.连接DG交BE于H.延长AH交BC于M.交DE于N．求证:BM2=MG•MC,(3)如图3.� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

9．如图1，在△ABC中，AB=5，BC=6，AC=4，点D从A出发，在AB边上以每秒1个单位的速度向B运动，过点D作DE∥BC交AC于E，过点D作DF∥AC交BC于F，运动时间为t秒．
（1）当t为何值时，四边形DFCE为菱形；
（2）如图2，G为边BC上任一点，连接DG交BE于H，延长AH交BC于M，交DE于N．求证：BM²=MG•MC；
（3）如图3，点M为边BC上，AM交DF于P，若BM：MC=3：2，当t为何值时，点P恰好为MN的中点？

分析（1）先由平行线的性质得出比例式，四边形DFCE是平行四边形；当四边形DFCE为菱形时，DE=CE，求出DE，AD，即可得出t的值；
（2）根据平行线的性质得出比例式，由比例式相等证出结论；
（3）先求出BM、MC，再由点P为MN的中点，得出DN=MF，得出关于t的方程，解方程即可．

解答解：（1）∵DE∥BC，DF∥AC，
∴四边形DFCE是平行四边形，$\frac{DE}{BC}=\frac{AE}{AC}$，$\frac{DE}{BC}=\frac{AD}{AB}$，
当四边形DFCE为菱形时，DE=CE，
∴$\frac{DE}{6}=\frac{4-DE}{4}$，
解得：DE=$\frac{12}{5}$，
∴$\frac{AD}{5}=\frac{\frac{12}{5}}{6}$，
∴AD=2，
∴t=2时，四边形DFCE为菱形；
（2）设BE交DG于O，如图2所示：
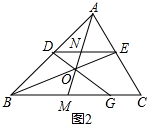∵DE∥BC，
∴$\frac{BM}{NE}=\frac{OB}{OE}$=$\frac{OM}{ON}=\frac{MG}{DN}$，$\frac{MC}{NE}=\frac{AC}{AE}$=$\frac{AM}{AN}=\frac{BM}{DN}$，
∴$\frac{BM}{MG}=\frac{NE}{DN}$，$\frac{MC}{BM}=\frac{NE}{DN}$，
∴$\frac{BM}{MG}=\frac{MC}{BM}$，
∴BM²=MG•MC；
（3）∵BM：MC=3：2，BC=6，
∴BM=$\frac{18}{5}$，MC=$\frac{12}{5}$，
∵DE∥BC，若点P为MN的中点，则DN=MF，
$\frac{DE}{BC}=\frac{AD}{AB}$，$\frac{DN}{BM}=\frac{AD}{AB}$，
即$\frac{DE}{6}=\frac{t}{5}$，$\frac{DN}{\frac{18}{5}}=\frac{t}{5}$，
∴DE=$\frac{6}{5}$t，DN=$\frac{18}{25}$t，
∴CF=DE=$\frac{6}{5}$t，
∴MF=$\frac{12}{5}$-$\frac{6}{5}$t，
∴$\frac{18}{25}t=\frac{12}{5}-\frac{6}{5}t$，
解得：t=$\frac{5}{4}$．
即t=$\frac{5}{4}$时，点P恰好为MN的中点．

点评本题是相似形综合题，考查了平行四边形的判定、菱形的性质、平行线分线段成比例定理、等积式的证法等知识；本题综合性强，难度较大，特别是（3）中，根据题意列出关于t的方程是解决问题的关键．

练习册系列答案