
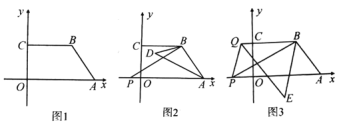
【题目】在平面直角坐标系中,四边形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上,顶点B 在第一象限,OA//CB.
(1)如图 1,若点 A(6,0),B(4,3),点 M 是 y 轴上一点,且 SBCM SAOM ,求点 M的坐标;
(2)如图 2,点 P 是 x 轴上点 A 左边的一点,连接 PB,∠PBC 和∠PAB 的角平分线交于点D,求证:∠ABP+2∠ADB=180°;
(3)如图 3,点 P 是 x 轴上点 A 左边的一点,点 Q 是射线 BC 上一点,连接 PB、PQ,∠ABP和∠BQP 的平分线相交于点 E,求![]() 的值.
的值.
【答案】(1)(0,![]() )或(0,
)或(0,![]() );(2)见解析;(3)2
);(2)见解析;(3)2
【解析】
(1)首先根据题意可判断点M一定在点C的下方,接下来分类两种情况讨论:当0<m<3及m<0时,根据SBCM SAOM及三角形的面积公式列出方程计算即可
(2)过点D作DH∥BC,根据平行线的性质可证得∠ADB=∠DAO+∠DBC,再根据角平分线可得∠PBC+∠PAB=2∠ADB,最后再根据两直线平行同旁内角互补即可得证;
(3)先设∠ABF=∠EBG=x,∠GQP=∠EQB=y,根据三角形的内角和及平行线的性质可分别证得∠BEQ-∠BAP=x-y,∠BPQ-∠BEQ=x-y,等量代换即可求得答案.
(1)解:设点M的坐标为(0,m),
∵点 A(6,0),B(4,3),
∴AO=6,BC=4,
∵SBCM SAOM,
∴点M一定在点C的下方,
当0<m<3时,
则![]() ,
,
解得![]() ,
,
∴点M的坐标为(0,![]() ),
),
当m<0时,
则![]() ,
,
解得![]() ,
,
∴点M的坐标为(0,![]() ),
),
综上所述,点M的坐标为(0,![]() )或(0,
)或(0,![]() );
);
(2)证明:如图,过点D作DH∥BC,
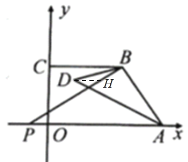
∵DH∥BC,OA∥BC,
∴DH∥OA,
∴∠HAD=∠DAO,
∵DH∥BC,
∴∠HAB=∠DBC,
∴∠ADB=∠HAD+∠HAB
=∠DAO+∠DBC,
∵DB、DA分别平分∠PBC、∠PAB,
∴∠PBC=2∠DBC,∠PAB=2∠DAO,
∴∠PBC+∠PAB=2(∠DBC+∠DAO)
=2∠ADB,
∵OA∥BC,
∴∠PAB+∠ABC=∠PAB+∠PBC+∠ABP=180,
即2∠ADB+∠ABP=180°;
(3)解:如图,
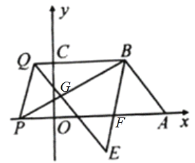
∵∠ABP和∠BQP
∴设∠ABF=∠EBG=x,∠GQP=∠EQB=y,
∵OA∥BC,
∴∠AFB=∠EBQ,
∴180°-(∠ABF+∠BAP)= 180°-(∠BEQ+∠EQB)
∴∠ABF+∠BAP=∠BEQ+∠EQB,
即:x+∠BAP=∠BEQ+y,
∴x-y=∠BEQ-∠BAP,
∵∠EBG +∠BEQ+∠BGE=∠GQP+∠BPQ+∠PGQ=180°,∠BGE=∠PGQ,
∴∠EBG +∠BEQ =∠GQP+∠BPQ,
即:x+∠BEQ=y+∠BPQ,
∴x-y=∠BPQ-∠BEQ,
∴∠BPQ-∠BEQ=∠BEQ-∠BAP,
即∠BPQ+∠BAP=2∠BEQ,
∴![]() ,
,
∴![]() 的值为2.
的值为2.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,P1、P2(P2在P1的右侧)是y= ![]() (k>0)在第一象限上的两点,点A1的坐标为(2,0).
(k>0)在第一象限上的两点,点A1的坐标为(2,0).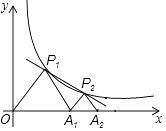
(1)填空:当点P1的横坐标逐渐增大时,△P1OA1的面积将(减小、不变、增大)
(2)若△P1OA1与△P2A1A2均为等边三角形,
①求反比例函数的解析式;
②求出点P2的坐标,并根据图象直接写在第一象限内,当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y= ![]() 的函数值.
的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比学习:
一动点沿着数轴向右平移![]() 个单位,再向左平移
个单位,再向左平移![]() 个单位,相当于向右平移
个单位,相当于向右平移![]() 个单位.用有理数加法表示为
个单位.用有理数加法表示为![]() .若坐标平面上的点做如下平移:沿
.若坐标平面上的点做如下平移:沿![]() 轴方向平移的数量为
轴方向平移的数量为![]() (向右为正,向左为负,平移
(向右为正,向左为负,平移![]() 个单位),沿
个单位),沿![]() 轴方向平移的数量为
轴方向平移的数量为![]() (向上为正,向下为负,平移
(向上为正,向下为负,平移![]() 个单位),则把有序数对
个单位),则把有序数对![]() 叫做这一平移的“平移量”;“平移量”
叫做这一平移的“平移量”;“平移量”![]() 与“平移量”
与“平移量”![]() 的加法运算法则为
的加法运算法则为![]()
解决问题:
(1)计算:![]() ;
;
(2)动点![]() 从坐标原点
从坐标原点![]() 出发,先按照“平移量”
出发,先按照“平移量”![]() 平移到
平移到![]() ,再按照“平移量”
,再按照“平移量”![]() 平移到
平移到![]() :若先把动点
:若先把动点![]() 按照.“平移量”
按照.“平移量”![]() 平移到
平移到![]() ,再按照“平移量”
,再按照“平移量”![]() 平移,最后的位置还是
平移,最后的位置还是![]() 吗?在图1中画出四边形
吗?在图1中画出四边形![]() .
.
(3)如图2,一艘船从码头![]() 出发,先航行到湖心岛码头
出发,先航行到湖心岛码头![]() ,再从码头
,再从码头![]() 航行到码头
航行到码头![]() ,最后回到出发点
,最后回到出发点![]() .请用“平移量”加法算式表示它的航行过程.
.请用“平移量”加法算式表示它的航行过程.


解:(1)![]() ______;
______;
(2)答:______;
(3)加法算式:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,购买“黄金1号”王米种子,所付款金额y元与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则购买1千克“黄金1号”玉米种子需付款___元,购买4千克“黄金1号”玉米种子需___元.
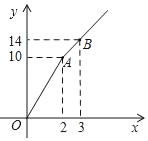
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
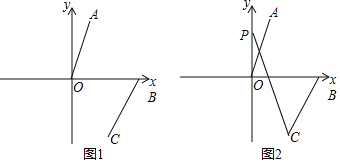
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则顶点A坐标是( )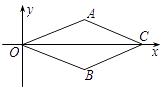
A.(2,1)
B.(1,﹣2)
C.(1,2)
D.(2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点E为AB边上的一个动点.
(1)如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC,连结AD.试比较∠DAC与∠B的大小,并说明理由;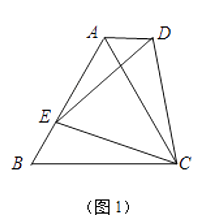
(2)如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC,且△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由;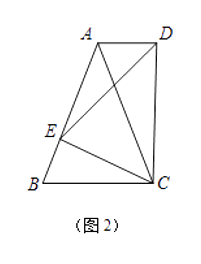
(3)如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上;
②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.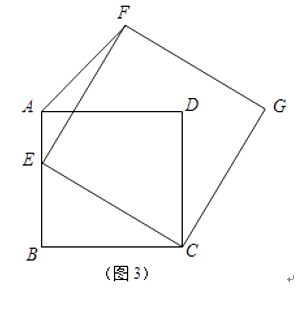
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com