
【题目】(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究. (操作)如图,在矩形ABCD中,AD=6,AB=4,点P是BC边上一点,现将△APB沿AP对折,得△APM,显然点M位置随P点位置变化而发生改变
(问题)试求下列几种情况下:点M到直线CD的距离
(1)∠APB=75°;
(2)P与C重合;
(3)P是BC的中点.
【答案】
(1)解:当∠APB=75°时,如图1,过M作EF⊥AD,则EF⊥BC,
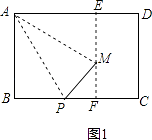
∵∠AMP=∠B=∠MFP=90°,
∴∠AME=∠MPF,
∴△AEM∽△MFP,
∵∠APB=75°,
∴∠MPF=30°,
∵AM=AB=4,
∴AE=2,
∴DE=4
(2)解:当P与C重合,如图2,过M作GH∥AD交BA,CD的延长线于G,H,
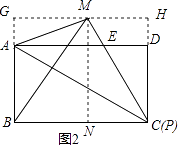
则四边形ADHG是矩形,
∵∠AMP=∠ABC=∠AMC=90°,
∴∠AMG=∠MPH,
∴△AMG∽△MHP,
设AG=x,则DH=x,
∴PH=4+x,
∴ ![]() ,
,
∴MH= ![]() x,
x,
在Rt△MHP中,MH2+PH2=MC2,
即( ![]() x)2+(4x)2=62,
x)2+(4x)2=62,
∴x= ![]() (负值舍去),
(负值舍去),
∴MH= ![]()
(3)解:当P是BC的中点时,如图3,过M作EF∥AB交AB,BC于E,F,
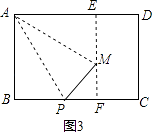
∵P是BC的中点,
∴BP=3,
设PF=x,则BF=3+x,
∴AE=3+x,
由折叠的性质得,AM=AB=4,PM=PB=3,∠AMP=∠B=90°,
∴△AEM∽△MFP,
∴ ![]() ,
,
∴EM= ![]() x,
x,
在Rt△AEM中,
AE2+EM2=AM2,
即( ![]() x)2+(3+x)2=42,
x)2+(3+x)2=42,
∴x= ![]() (负值舍去),
(负值舍去),
∴DE= ![]() .
.
【解析】(1)如图1,过M作EF⊥AD,则EF⊥BC,由∠AMP=∠B=∠MFP=90°,得到∠AME=∠MPF,推出△AEM∽△MFP,根据已知条件得到∠MPF=30°,AE=2,即可得到结论;(2)如图2,过M作GH∥AD交BA,CD的延长线于G,H,则四边形ADHG是矩形,推出△AMG∽△MHP,设AG=x,则DH=x,得到PH=4+x,列比例式得到MH= ![]() x,根据勾股定理得到x=
x,根据勾股定理得到x= ![]() (负值舍去),即可得到结论;(3)当P是BC的中点时,如图3,过M作EF∥AB交AB,BC于E,F,推出△AEM∽△MFP,根据相似三角形的性质得到
(负值舍去),即可得到结论;(3)当P是BC的中点时,如图3,过M作EF∥AB交AB,BC于E,F,推出△AEM∽△MFP,根据相似三角形的性质得到 ![]() ,得到EM=
,得到EM= ![]() x,根据勾股定理列方程即可得到结论.
x,根据勾股定理列方程即可得到结论.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE. 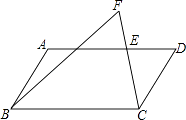
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个棱长为![]() 的正方体的每个面等分成
的正方体的每个面等分成![]() 个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去
个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去![]() 个小正方体),所得到的几何体的表面积是( )
个小正方体),所得到的几何体的表面积是( )

A. 78 B. 72 C. 54 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负).
A 组 | ﹣1.5 | +1.5 | ﹣1 | ﹣2 | ﹣2 |
B组 | +1 | +3 | ﹣3 | +2 | ﹣3 |
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰三角形ABO的底边OA在x轴上,顶点B在反比例函数y= ![]() (x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=
(x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y= ![]() (x>0)的图象上滑动,但点O始终位于原点.
(x>0)的图象上滑动,但点O始终位于原点.
(1)如图①,若点A的坐标为(6,0),求点B的坐标;
(2)当点A移动到什么位置时,三角形ABO变成等腰直角三角形,请说明理由;
(3)在(2)中,如图②,△PA1A是等腰直角三角形,点P在反比例函数y= ![]() (x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
(x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
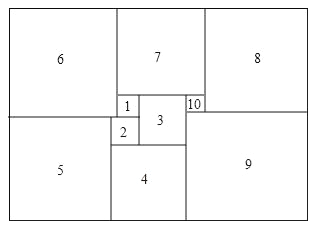
【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,请你计算:
(1)如果标注1、2的正方形边长分别为1,2,第3个正方形的边长= ;第5个正方形的边长= ;
(2)如果标注1、2的正方形边长分别为x,y,第10个正方形的边长= .(用含x、y的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园准备修建一块长方形草坪,长为30米,宽为20米.并在草坪上修建如图所示的十字路,已知十字路宽![]() 米,回答下列问题:
米,回答下列问题:
(1)修建十字路的面积是多少平方米?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com