
 (2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC.
(2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC.| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
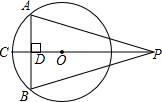 (2004•西藏)如图,P是⊙O外一点,PO的延长线交⊙O于C,AB是⊙O的弦,且AB⊥PC,连结PA、PB,根据这些已知条件,不再添加辅助线,写出你能得出的三个结论:
(2004•西藏)如图,P是⊙O外一点,PO的延长线交⊙O于C,AB是⊙O的弦,且AB⊥PC,连结PA、PB,根据这些已知条件,不再添加辅助线,写出你能得出的三个结论: |
| AC |
 |
| BC |
 |
| AC |
 |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
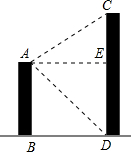 (2004•西藏)如图,在大街的两侧分别有甲、乙两栋楼房AB、CD,已知甲楼AB的高为30cm,在楼顶A处测得乙楼CD的楼顶C的仰角(即图中∠EAC)为30°,测得乙楼楼底D的俯角(即图中∠EAD)为45°,求乙楼的高CD(精确到1m,参考数据
(2004•西藏)如图,在大街的两侧分别有甲、乙两栋楼房AB、CD,已知甲楼AB的高为30cm,在楼顶A处测得乙楼CD的楼顶C的仰角(即图中∠EAC)为30°,测得乙楼楼底D的俯角(即图中∠EAD)为45°,求乙楼的高CD(精确到1m,参考数据| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
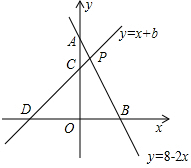 (2004•西藏)已知,如图,直线y=8-2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO).
(2004•西藏)已知,如图,直线y=8-2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com