
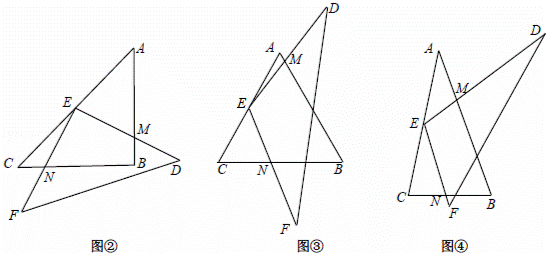
如图①,△ABC与△DEF是将△ACF沿过A点的某条直线剪开得到的(AB,DE是同一条剪切线).平移△DEF使顶点E与AC的中点重合,再绕点E旋转△DEF,使ED,E F分别与AB,BC交于M,N两点.
F分别与AB,BC交于M,N两点.
(1)如图②,△ABC中,若AB=BC,且∠ABC=90°,则线段EM与EN有何数量关系?请直接写出结论;
(2)如图③,△ABC中,若AB=BC,那么(1)中的结论是否还成立?若成立,请给出证明:若不成立,请说明理由;
(3)如图④,△ABC中,若AB:BC=m:n,探索线段EM与EN的数量关系,并证明你的结论.
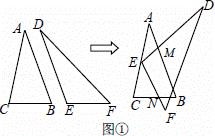
解:(1)EM=EN.
证明:过点E作EG⊥BC,G为垂足,作EH⊥AB,H为垂足,连接BE,如答图②所示.
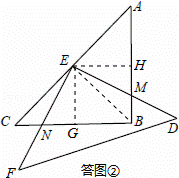
则∠EHB=∠EGB=90°.
∴在四边形BHEG中,∠HBG+∠HEG=180°.
∵∠HBG+∠DEF=180°,
∴∠HEG=∠DEF.
∴∠HEM=∠GEN.
∵BA=BC,点E为AC中点,
∴BE平分∠ABC.
又∵EH⊥AB,EG⊥BC,
∴EH=EG.
在△HEM和△GEN中,
∵∠ HEM=∠GEN,EH=EG,∠EHM=∠EGN,
HEM=∠GEN,EH=EG,∠EHM=∠EGN,
∴△HEM≌△GEN.
∴EM=EN.
(2)EM=EN仍然成立.
证明:过点E作EG⊥BC,G为垂足,作EH⊥AB,H为垂足,连接BE,如答图③所示.

则∠EHB=∠EGB=90°.
∴在四边形BHEG中,∠HBG+∠HEG=180°.
∵∠HBG+∠DEF=180°,
∴∠HEG=∠DEF.
∴∠HEM=∠GEN.
∵BA=BC,点E为AC中点,
∴BE平分∠ABC.
又∵EH⊥AB,EG⊥BC,
∴EH=EG.
在△HEM和△GEN中,
∵∠HEM=∠GEN,EH=EG,∠EHM=∠EGN,
∴△HEM≌△GEN.
∴EM=EN.
(3)线段EM与EN满足关系:EM:EN=n:m.
证明:过点E作EG⊥BC,G为垂足,作EH⊥AB,H为垂足,连接BE,如答图④所示.
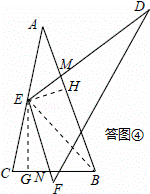
则∠EHB=∠EGB=90°.
∴在四边形BHEG中,∠HBG+∠HEG=180°.
∵∠HBG+∠DEF=180°,
∴∠HEG=∠DEF.
∴∠HEM=∠GEN.
∵∠HEM= ∠GEN,∠EHM=∠EGN,
∠GEN,∠EHM=∠EGN,
∴△HEM∽△GEN.
∴EM:EN=EH:EG.
∵点E为AC的中点,
∴S△AEB=S△CEB.
∴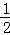 AB•EH=
AB•EH=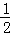 BC•EG.
BC•EG.
∴EH:EG=BC:AB.
∴EM:EN=BC:AB.
∵AB:BC=m:n,
∴EM:EN=n:m.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
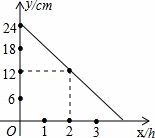
在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系中,点A的坐标为(﹣1,2),点C的坐标为(﹣3,0),将点C绕点A逆时针旋转90°,再向下平移3个单位,此时点C的对应点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
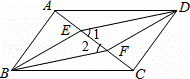
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列运算正确的是( )
|
| A. | a2+a3=a5 | B. | (﹣2a2)3=﹣6a6 | C. | (2a+1)(2a﹣1)=2a2﹣1 | D. | (2a3﹣a2)÷a2=2a﹣1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,将一个边长为a的 正方形纸片剪去两个小矩形,得到一个“
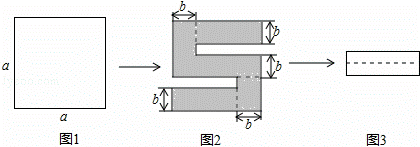
正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
|
| A. | 2a﹣3b | B. | 4a﹣8b | C. | 2a﹣4b | D. | 4a﹣10b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com