
如图,已知点A(−3,5)在抛物线y=![]() x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
1.求抛物线的解析式;
2.当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
3.试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.
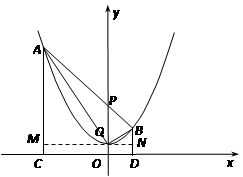
1.![]()
2.2或![]()
3.![]() 和4
和4![]()
解析:解:(1)把A(−3,5)代入得:5=![]() ´9+c,··········· 1’
´9+c,··········· 1’
∴c=![]() . 2’
. 2’
(2)①若AQ⊥BQ,过点Q作MN⊥y轴,
可证△AMQ∽△QNB.
∵AM=AC−MC=![]() ,MQ=3,
,MQ=3,
∴![]() .
.
设B(3k,2k+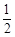 ),
),
代入抛物线解析式得:k=![]() ,即B(
,即B(![]() ,
,![]() ).·········· 3’
).·········· 3’
∴直线AB的解析式为:![]() .
.
∴OP=![]() ,∴PQ=2.······················· 4’
,∴PQ=2.······················· 4’
②若AQ⊥AB,
∵AC∥PQ,可证△AMQ∽△QAP,
又由勾股定理得AQ=![]() .
.
∴PQ=![]() .········· 6’
.········· 6’
∴对应的时刻t为:2或![]() .
.
(3)①若AC=BD,AP=BP,
此时点A与点B关于y轴对称,
∴OP=AC=5,
∴PQ=4![]() .·························· 8’
.·························· 8’
②若AC=AP,
设P(0,y),则:9+(y−5)2=25,
解之得,y=1,即OP=1.
∴PQ=![]() .··························· 9’
.··························· 9’
此时,直线AP解析式为:![]() .
.
与抛物线的交点B为(![]() ,
,![]() ),
),
∴PB=![]() =BD.···················· 10’
=BD.···················· 10’
∴满足条件的时刻为:![]() 和4
和4![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设| BA |
| a |
| BC |
| b |
| BD |
| a |
| b |
| a |
| b |
| BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com