
【题目】如图,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,
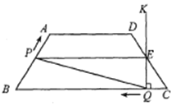
,![]() .点Р从点B出发沿折线段
.点Р从点B出发沿折线段![]() 以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段
以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段![]()
![]() 于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒
于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒![]() .
.
(1)点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点Р运动到AD上时,t为何值能使![]() ?
?
(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?
(4)![]() 能为直角三角形时t的取值范围________.(直接写出结果)
能为直角三角形时t的取值范围________.(直接写出结果)
(注:备用图不够用可以另外画)
【答案】(1) ![]() 秒,
秒,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)把BA,AD,DC它们的和求出来再除以速度每秒5个单位就可以求出t的值,然后也可以求出BQ的长;
(2)如图1,若PQ∥DC,又AD∥BC,则四边形PQCD为平行四边形,从而PD=QC,用t分别表示QC,BA,AP,然后就可以得出关于t的方程,解方程就可以求出t;
(3)分情况讨论,当P在BA上运动时,E在CD上运动.0≤t≤10,QC的长度≤30,PE的长度>AD=75,QC<PE,此时不能构成以P、Q、C、E为顶点的平行四边形;当P点运动到AD上,E在AD上,且P在E的左侧时,P、Q、C、E为顶点的四边形可能是平行四边形,根据平行四边形的性质建立方程求出其解就可以得出结论;当P在E点的右侧且在AD上时,t≤25,P、Q、C、E为直角梯形,当P在CD上,E在AD上QE与PC不平行,P、Q、C、E不可能为平行四边形,
(4)①当点P在BA(包括点A)上,即0<t≤10时,如图2.过点P作PG⊥BC于点G,则PG=PBsinB=4t,又有QE=4t=PG,易得四边形PGQE为矩形,此时△PQE总能成为直角三角形
②当点P、E都在AD(不包括点A但包括点D)上,即10<t≤25时,如图1.由QK⊥BC和AD∥BC可知,此时,△PQE为直角三角形,但点P、E不能重合,即5t-50+3t-30≠75,解得t≠![]() .③当点P在DC上(不包括点D但包括点C),即25<t≤35时,如图3.由ED>25×3-30=45,
.③当点P在DC上(不包括点D但包括点C),即25<t≤35时,如图3.由ED>25×3-30=45,
可知,点P在以QE=40为直径的圆的外部,故∠EPQ不会是直角.由∠PEQ<∠DEQ,可知∠PEQ一定是锐角.对于∠PQE,
∠PQE≤∠CQE,只有当点P与C重合,即t=35时,如图4,∠PQE=90°,△PQE为直角三角形.
解:(1)t=(50+75+50)÷5=35(秒)时,点P到达终点C,
此时,QC=35×3=105,
∴BQ的长为135105=30.
(2)如图1,若PQ∥DC,
∵AD∥BC,
∴四边形PQCD为平行四边形,
∴PD=QC,
由QC=3t,BA+AP=5t
得50+755t=3t,
解得t=![]() .
.
∴当t=![]() 时,PQ∥DC.
时,PQ∥DC.
(3)当P在BA上运动时,E在CD上运动.0t10,QC的长度30,PE的长度>AD=75,QC<PE,此时不能构成以P、Q、C. E为顶点的平行四边形;
当P点运动到AD上,E在AD上,且P在E的左侧时,P、Q、C. E为顶点的四边形是平行四边形,如图5,
∴PE=QC.
如图1,作DH⊥BC于H,AG⊥BC于G,
∠AGB=∠DHC=90
∴四边形AGHD是矩形,
∴GH=AD=75.AG=DH.
在△ABG和△DCH中,
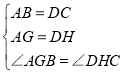
∴△ABG≌△DCH,
∴BG=CH=![]()
∴ED=3(t10)
∵AP=5t50,
∴PE=75(5t50)3(t10)=1558t.
∵QC=3t,
∴1558t=3t,
t=![]() .
.
当P在E点的右侧且在AD上时,t25,P、Q、C. E为直角梯形,
当P在CD上,E在AD上QE与PC不平行,P、Q、C. E不可能为平行四边形,
∴t=![]() ;
;
(4)①当点P在BA(包括点A)上,即0<t10时,如图2.
过点P作PG⊥BC于点G,则PG=PBsinB=4t,
又有QE=4t=PG,易得四边形PGQE为矩形,此时△PQE总能成为直角三角形。
②当点P、E都在AD(不包括点A但包括点D)上,即10<t25时,如图1.
由QK⊥BC和AD∥BC可知,此时,△PQE为直角三角形,但点P、E不能重合,
即5t50+3t30≠75,解得t≠![]() .③当点P在DC上(不包括点D但包括点C),
.③当点P在DC上(不包括点D但包括点C),
即25<t35时,如图3.由ED>25×330=45,可知,点P在以QE=40为直径的圆的外部,故∠EPQ不会是直角。由∠PEQ<∠DEQ,可知∠PEQ一定是锐角
对于∠PQE,∠PQE∠C, 只有当点P与C
重合,即t=35时,如图4,∠PQE=90,△PQE为直角三角形。
综上所述,当△PQE为直角三角形时,t的取值范围是0<t25且t≠![]() 或t=35.
或t=35.
故答案为:0<t25且t≠![]() 或t=35.
或t=35.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的![]() .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了解孩子们对《地理中国》 《最强大脑》 《挑战不可能》 《超级演说家》 《中国诗词大会》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
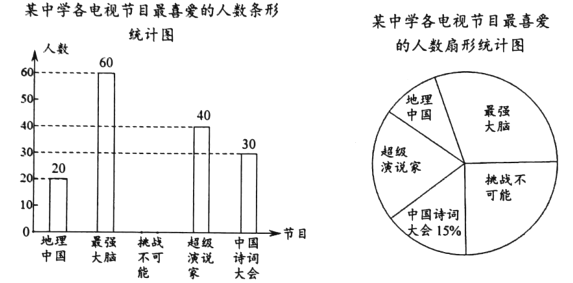
(1)本次调查共抽取了_________________名学生。
(2)补全条形统计图。
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是__________度。
(4)若该校有1500名学生,请估计喜爱《最强大脑》节目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点![]() 从
从![]() 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.

【1】点 (填M或N)能到达终点;
【1】求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
【1】是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,
![]() 说明理由.
说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,小丽用棋子摆成三角形的图案,观察下面图案并填空:

按照这样的方式摆下去,摆第5个三角形图案需要_____________枚棋子;摆第n个三角形图案需要_________枚棋子(用含有n的代数式表示);摆第99个三角形图案需要_______枚棋子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面“将无限循环小数化为分数”材料,并解决相应问题:
我们知道分数![]() 写为小数形式即为
写为小数形式即为![]() ,反之,无限循环小数
,反之,无限循环小数![]() 写成分数形式即
写成分数形式即![]() .一般地,任何一个无限循环小数都可以写成分数形式吗?如果可以,应怎样写呢?
.一般地,任何一个无限循环小数都可以写成分数形式吗?如果可以,应怎样写呢?
(发现)先以无限循环小数![]() 为例进行讨论.
为例进行讨论.
设![]() =x,由
=x,由![]() =0.777…可知,10x=7.777…,即10x﹣x=7.解方程,得x=
=0.777…可知,10x=7.777…,即10x﹣x=7.解方程,得x=![]() .于是
.于是![]() =
=![]() ,
,
(类比探究)再以无限循环小数![]() 为例,做进一步的讨论.
为例,做进一步的讨论.
无限循环小数![]() =0.737373…,它的循环节有两位,类比上面的讨论可以想到如下做法.
=0.737373…,它的循环节有两位,类比上面的讨论可以想到如下做法.
设![]() =x,由
=x,由![]() =0.737373…可知,100x=73.7373…,所以100x﹣x=73.解方程,得x=
=0.737373…可知,100x=73.7373…,所以100x﹣x=73.解方程,得x=![]() ,于是得
,于是得![]() =
=![]()
(解决问题)
(1)请你把无限小数![]() 写成分数形式,即
写成分数形式,即![]() = ;
= ;
(2)请你把无限小数![]() 写成分数形式,即
写成分数形式,即![]() = ;
= ;
(3)根据以上过程比较![]() 与1的大小关系,并说明你的理由.
与1的大小关系,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
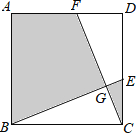
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示的数是-8,
点表示的数是-8,![]() 点表示的数是2.动线段
点表示的数是2.动线段![]() (点
(点![]() 在点
在点![]() 的右侧),从点
的右侧),从点![]() 与点
与点![]() 重合的位置出发,以每秒2个单位的速度向右运动,运动时间为
重合的位置出发,以每秒2个单位的速度向右运动,运动时间为![]() 秒.
秒.
![]()
(1)①已知点![]() 表示的数是-6,试求点
表示的数是-6,试求点![]() 表示的数;
表示的数;
②用含有![]() 的代数式表示点
的代数式表示点![]() 表示的数;
表示的数;
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)试问当线段![]() 在什么位置时,
在什么位置时,![]() 或
或![]() 的值始终保持不变?请求出它的值并说明此时线段
的值始终保持不变?请求出它的值并说明此时线段![]() 的位置.
的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
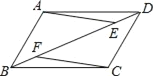
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com