
【题目】如图,已知,∠ABG为锐角,AH∥BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为F(F不与A重合),若∠ECF=n°,则∠BAF的度数为_____度.(用n来表示)

【答案】n或180﹣n
【解析】
分两种情况讨论:当点![]() 在线段
在线段![]() 上;点
上;点![]() 在
在![]() 延长线上,根据平行线的性质,即可得到结论.
延长线上,根据平行线的性质,即可得到结论.
解:过A作AM⊥BC于M,如图1,
当点C在BM延长线上时,点F在线段AD上,
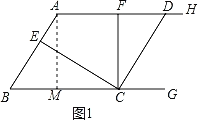
∵AD∥BC,CF⊥AD,
∴CF⊥BG,
∴∠BCF=90°,
∴∠BCE+∠ECF=90°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠B+∠BCE=90°,
∴∠B=∠ECF=n°,
∵AD∥BC,
∴∠BAF=180°﹣∠B=180°﹣n°,
过A作AM⊥BC于M,如图2,当点C在线段BM上时,点F在DA延长线上,
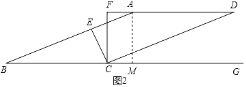
∵AD∥BC,CF⊥AD,
∴CF⊥BG,
∴∠BCF=90°,
∴∠BCE+∠ECF=90°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠B+∠BCE=90°,
∴∠B=∠ECF=n°,
∵AD∥BC,
∴∠BAF=∠B=n°,
综上所述,∠BAF的度数为n°或180°﹣n°,
故答案为:n或180﹣n.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
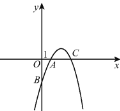
【题目】如图,抛物线y=-x2+5x+n与x轴交于点A(1,0)和点C,与y轴交于点B.
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
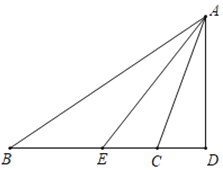
【题目】如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形的纸片ABCD中,AD=3cm,AB=4cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F.
(1)图中有等腰三角形吗?说明理由.
(2)求重叠部分(即△ACF)的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 的边长为
的边长为![]() ,
,![]() 是边
是边![]() 上的动点,
上的动点,![]() 交边
交边![]() 于点
于点![]() ,在边
,在边![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请直接写出图中与线段![]() 相等的两条线段;(不再另外添加辅助线)
相等的两条线段;(不再另外添加辅助线)
(2)探究:当点![]() 在什么位置时,四边形
在什么位置时,四边形![]() 是平行四边形?并判断四边形
是平行四边形?并判断四边形![]() 是什么特殊的平行四边形,请说明理由;
是什么特殊的平行四边形,请说明理由;
(3)在(2)的条件下,以点![]() 为圆心,
为圆心,![]() 为半径作圆,根据
为半径作圆,根据![]() 与平行四边形
与平行四边形![]() 四条边交点的总个数,求相应的
四条边交点的总个数,求相应的![]() 的取值范围.
的取值范围.
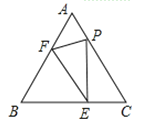
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,E为BC延长线上一点.
(1)请你添加平行线证明:∠ACE=∠ABC+∠A.
(2)如图2,若点D是线段AC上一点,且DF∥BC,作DG平分∠BDF交AB于G,DH平分∠GDC交BC于H,且∠BDC比∠ACB大20°,求∠GDH的度数.
(3)如图3,已知E为BC延长线上一点,D是线段AC上一点,连接DE,若∠ABC的平分线与∠ADE的平分线相交于点P,请你判断∠P、∠A、∠E的数量关系并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:
﹣2,4,﹣8,16,﹣32,64,…; ①
﹣1,2,﹣4,8,﹣16,32,…; ②
0,6,﹣6,18,﹣30,66,…;③
(1)第①行数中的第n个数为 (用含n的式子表示)
(2)取每行数的第n个数,这三个数的和能否等于﹣318?如果能,求出n的值;如果不能,请说明理由.
(3)如图,用一个矩形方框框住六个数,左右移动方框,若方框中的六个数之和为﹣156,求方框中左上角的数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com