
【题目】如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.
①若OE=![]() ,OG=1,求
,OG=1,求![]() 的值;
的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
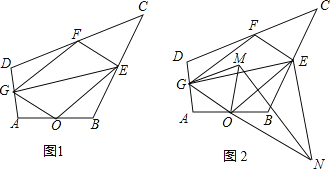
【答案】(1)证明见解析;(2)①![]() ;②添加AC=BD.
;②添加AC=BD.
【解析】(1)连接AC,由四个中点可知OE∥AC、OE=![]() AC,GF∥AC、GF=
AC,GF∥AC、GF=![]() AC,据此得出OE=GF、OE//GF,即可得证;
AC,据此得出OE=GF、OE//GF,即可得证;
(2)①由旋转性质知OG=OM、OE=ON,∠GOM=∠EON,据此可证△OGM∽△OEN得![]() ;
;
②连接AC、BD,根据①知△OGM∽△OEN,若要GM=EN只需使△OGM≌△OEN,添加使AC=BD的条件均可以满足此条件.
(1)如图1,连接AC,
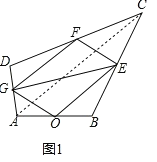
∵点O、E、F、G分别是AB、BC、CD、AD的中点,
∴OE∥AC、OE=![]() AC,GF∥AC、GF=
AC,GF∥AC、GF=![]() AC,
AC,
∴OE=GF,OE//GF,
∴四边形OEFG是平行四边形;
(2)①∵△OGE绕点O顺时针旋转得到△OMN,
∴OG=OM、OE=ON,∠GOM=∠EON,
∴![]() ,
,
∴△OGM∽△OEN,
∴![]() ;
;
②添加AC=BD,
如图2,连接AC、BD,
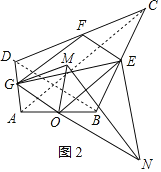
∵点O、E、F、G分别是AB、BC、CD、AD的中点,
∴OG=EF=![]() BD、OE=GF=
BD、OE=GF=![]() BD,
BD,
∵AC=BD,
∴OG=OE,
∵△OGE绕点O顺时针旋转得到△OMN,
∴OG=OM、OE=ON,∠GOM=∠EON,
∴OG=OE、OM=ON,
在△OGM和△OEN中,
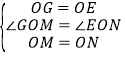 ,
,
∴△OGM≌△OEN(SAS),
∴GM=EN.


科目:初中数学 来源: 题型:
【题目】如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点C出发.以每秒1个单位长度的速度沿CB匀速运动,动点Q从点D出发,以每秒2个单位长度的速度沿x轴的负方向匀速运动,P,Q两点同时运动,当Q点到达O点时两点同时停止运动.设运动时间为t秒,
(1)当t为何值时,四边形OCPQ为矩形?
(2)当t为何值时,以C,P,Q,A为顶点的四边形为平行四边形?
(3)E点坐标(5,0),当△OEP为等腰三角形时,请直接写出所有符合条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
在数学课上,老师提出如下问题:
己知:已知:Rt△ABC,∠ABC=90°.
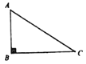
求作:矩形ABCD.
小敏的作法如下:
①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;
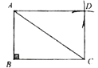
②连接DA、DC;所以四边形ABCD为所求矩形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.

(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园,并比小明早到达,已知爸爸的平均速度是小明从家到中心书城平均速度的两倍.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
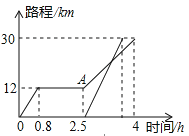
(1)小明家到滨海公园的路程为 km,小明在中心书城逗留的时间为 h;
(2)小明从中心书城到滨海公园的平均速度是 km/h,
(3)小明爸爸比小明早到达多长时间?
(4)爸爸驾车经过多长时间追上小明?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造□PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.

(1)求证:四边形ADEC是平行四边形;
(2)以线段PE为对角线作正方形MPNE,点M、N分别在第一、四象限.
①当点M、N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M、N中恰好只有一点落在四边形ADEC的内部(不包括边界)时,设□PCOD的面积为S,直接写出S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
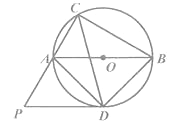
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com