
【题目】如图,已知直线y=3x+3与x轴交于点A,与y轴交于点C,过点C的直线y=﹣x+b与x轴交于点B.
(1)b的值为______;
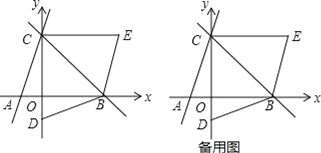
(2)若点D的坐标为(0,﹣1),将△BCD沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形;
(3)在直线BC上是否存在点P,使得以P、A、D、B为顶点的四边形是平行四边形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】(1)3;(2)证明见解析;(3)存在,P1(4,-1),P2(2,1)
【解析】分析:(1)先由点C在直线y=3x+3上,求出点C坐标,代入直线y=-x+b中即可.(2)先求出∠OBC=∠OCB=45°,进而判断出CE∥AB,最后判断出CE=AB 即可;(3)方法①先确定出直线AD,BC解析式,进而判断出AD∥BC,使得以P、A、D、B为顶点的四边形是平行四边形,只要AD=PB即可.
本题解析: (1)∵直线y=3x+3与x轴交于点A,与y轴交于点C,
∴C(0,3),
∵过点C的直线y=x+b与x轴交于点B,
∴b=3,
故答案为3,
(2)证明:当b=3时,直线BC为y=x+3
由x=0得,y=3,
∴C(0,3),OC=3
由y=0得,x=3,
∴B(3,0),OB=3
∴OB=OC=3
∴∠OBC=∠OCB=45°
由折叠得:∠BCE=∠OCB=45°
CE=CD=OC+OD=4
∴∠OBC=∠BCE
∴CE∥AB
由y=3x+3,令y=0得,x=1,
∴A(1,0)
∴AB=OA+OB=3+1=4
∴AB=CE
∴四边形ABEC为平行四边形。
(3)存在点P,使以P、A、 D、 B为顶点的四边形是平行四边形。
如图,

∵A(1,0)、D(0,1),
∴直线AD解析式为y=x1,
∵B(3,0),C(0,3),
∴直线BC解析式为y=x+3.
∴AD∥BC,
∵点P在直线BC上,
∴设点P坐标为(m,m+3),
∴![]() ,
,
∵使得以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴P(2,1)或P(4,1),
综上所述,存在点P,使以P、A、D、 B为顶点的四边形是平行四边形。点P的坐标为![]() (2,1)或
(2,1)或![]() (4,1).
(4,1).


科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题。
我们知道方程![]() 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由![]() ,得
,得![]() ,(
,( ![]() 、
、![]() 为正整数)
为正整数)
![]() 则有
则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为整数.
为整数.
由2与3互质,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .
.
![]() 的正整数解为
的正整数解为![]()
问题:(1)若![]() 为自然数,则满足条件的
为自然数,则满足条件的![]() 值有_____________个
值有_____________个
(2)请你写出方程![]() 的所有正整数解:_________________________
的所有正整数解:_________________________
(3)若![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出它的所有整数解。
,并求出它的所有整数解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国对“一带一路”沿线国家不断加大投资,目前已为有关国家创造了近1100000000 美元税收,其中1100000000 用科学记数法表示应为( )
A. 0.11108B. 1.11010C. 1.1109D. 11108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x3﹣x=x(x2﹣1)B. ﹣a2+6a﹣9=﹣(a﹣3)2
C. x2+y2=(x+y)2D. a3﹣2a2+a=a(a+1)(a﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com