
分析 ①先将减法转化为加法,然后根据有理数加法的计算方法即可解答本题;
②先通分,然后进行计算即可解答本题;
③根据有理数的乘法可以解答本题;
④根据乘法分配律可以解答本题;
⑤根据乘法分配律可以解答本题;
⑥根据乘法分配律可以解答本题.
解答 解:①(-7)-(+5)+(-4)-(-10)
=(-7)+(-5)+(-4)+10
=-6;
②-$\frac{1}{4}$+$\frac{5}{6}$+$\frac{2}{3}$-$\frac{1}{2}$
=$-\frac{3}{12}+\frac{10}{12}+\frac{8}{12}-\frac{6}{12}$
=$\frac{3}{4}$;
③(-0.375)×1$\frac{1}{7}$×1$\frac{1}{2}$×(-2$\frac{1}{3}$)
=$\frac{3}{8}×\frac{8}{7}×\frac{3}{2}×\frac{7}{3}$
=$\frac{3}{2}$;
④(1-$\frac{4}{9}$+$\frac{5}{6}$-$\frac{7}{12}$)×(-36)
=1×(-36)-$\frac{4}{9}×(-36)+\frac{5}{6}×(-36)-\frac{7}{12}×(-36)$
=(-36)+16+(-30)+21
=-29;
⑤-14×$\frac{3}{4}$-0.34×$\frac{3}{7}$+$\frac{1}{4}$×(-14)+$\frac{4}{7}$×(-0.34)
=(-14)×($\frac{3}{4}+\frac{1}{4}$)+(-0.34)×($\frac{3}{7}+\frac{4}{7}$)
=(-14)+(-0.34)
=-14.34;
⑥5×(-19$\frac{18}{19}$)
=5×(-20+$\frac{1}{19}$)
=5×(-20)+5×$\frac{1}{19}$
=-100+$\frac{5}{19}$
=-99$\frac{14}{19}$.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+4x-3交x轴于A、B两点,与y轴交于点C,连AC,点P为第四象限抛物线上一点,且∠PCB=∠ACO,求点P的坐标.
如图,抛物线y=-x2+4x-3交x轴于A、B两点,与y轴交于点C,连AC,点P为第四象限抛物线上一点,且∠PCB=∠ACO,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
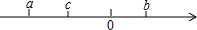 我们知道:正数的绝对值是它本身,不改变前面的符号.负数的绝对值是它的相反数,改变前面的符号.去绝对值符号时,绝对值符号里面如果是几个数的和或差时应加括号.若有理数a、b、c在数轴上的位置如图所示:
我们知道:正数的绝对值是它本身,不改变前面的符号.负数的绝对值是它的相反数,改变前面的符号.去绝对值符号时,绝对值符号里面如果是几个数的和或差时应加括号.若有理数a、b、c在数轴上的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\sqrt{2}$=2$\sqrt{2}$ | B. | $\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{{3}^{2}}$-$\sqrt{{2}^{2}}$=3-2=1 | ||
| C. | $\sqrt{8}$-2$\sqrt{2}$=0 | D. | $\sqrt{(1-\sqrt{3})^{2}}$=1-$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com