
已知点C为线段AB上一点, 分别以AC、BC为边在线段AB同侧作△ACD
和△BCE, 且CA=CD, CB=CE, ∠ACD=∠BCE, 直线AE与BD交于点F.
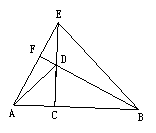
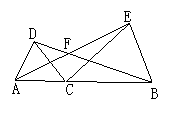

图1 ![]()
![]() 图2 图3
图2 图3
(1)如图1,求证:△ACE≌△DCB。
(2)如图1, 若∠ACD=60°, 则∠AFB= ;
如![]() 图2, 若∠ACD=90
图2, 若∠ACD=90![]() °, 则∠AFB= ;
°, 则∠AFB= ;
(3)如图3, 若∠ACD=β, 则∠AFB= ![]() (用含β的式子表示)
(用含β的式子表示)
并说明理![]() 由。
由。
解:(1)点B(3![]() ,-
,-![]() )----------------------------2分
)----------------------------2分
(2)O′(-![]() ,0) A′(0,-
,0) A′(0,-![]() )
)
B′(2![]() ,-
,-![]() ) C′(
) C′(![]() ,0)-------------------6分
,0)-------------------6分
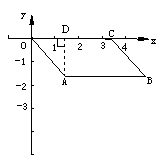 (3)S=
(3)S=![]()
=![]() -
-![]() ---
---![]() ---------------8分
---------------8分
=6 -------------------9分
∴△ACE≌△DCB(SAS) ![]()
∴∠CDB=∠CAE------------------10分
∵CA=CD
∴∠CAD=∠CDA
∵∠AFB=∠CDB+∠![]() CDA+∠DAF
CDA+∠DAF
∴∠AFB=∠CAE+∠CDA+∠D![]() AF=∠CDA+∠CAD ------------------11分
AF=∠CDA+∠CAD ------------------11分
∵∠DAC+∠CDA+∠ACD=180°
∴∠CDA+∠CA![]() D=180°-∠ACD=180º-β
D=180°-∠ACD=180º-β
即∠AFB=180º-β---![]() ---------------12分
---------------12分


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
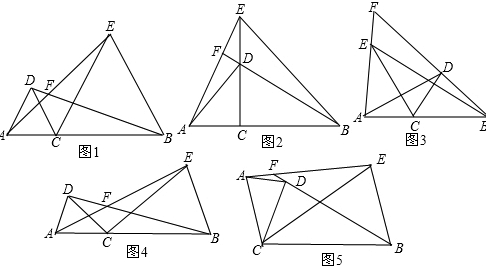
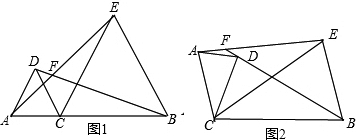 在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com