
 如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )| A. | 在一个角的内部,且到角两边的距离相等的点在这个角的平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 三角形三条角平分线的交点到三条边的距离相等 | |
| D. | 以上均不正确 |
科目:初中数学 来源: 题型:解答题
 类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.
类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离为y千米,图中的折线表示y与x之间的关系.根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知D、E和F、G分别在△ABC的AB、AC上,DF∥EG∥BC,AD:DE:EB=1:2:3,则S梯形DEGF:S梯形EBCG=8:27.
如图,已知D、E和F、G分别在△ABC的AB、AC上,DF∥EG∥BC,AD:DE:EB=1:2:3,则S梯形DEGF:S梯形EBCG=8:27.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
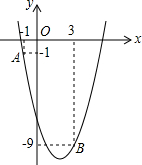 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,-1)和点B(3,-9).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com