
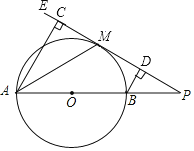
【题目】如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是___________.(写出所有正确结论的序号)
①AM平分∠CAB;
②AM2=ACAB;
③若AB=4,∠APE=30°,则![]() 的长为
的长为![]() ;
;
④若AC=3,BD=1,则有CM=DM=![]() .
.
【答案】①②④
【解析】
连接OM,由切线的性质可得OM⊥PC,继而得OM∥AC,再根据平行线的性质以及等边对等角即可求得∠CAM=∠OAM,由此可判断①;通过证明△ACM∽△AMB,根据相似三角形的对应边成比例可判断②;求出∠MOP=60°,利用弧长公式求得![]() 的长可判断③;由BD⊥PC,AC⊥PC,OM⊥PC,可得BD∥AC//OM,继而可得PB=OB=AO,PD=DM=CM,进而有OM=2BD=2,在Rt△PBD中,PB=BO=OM=2,利用勾股定理求出PD的长,可得CM=DM=DP=
的长可判断③;由BD⊥PC,AC⊥PC,OM⊥PC,可得BD∥AC//OM,继而可得PB=OB=AO,PD=DM=CM,进而有OM=2BD=2,在Rt△PBD中,PB=BO=OM=2,利用勾股定理求出PD的长,可得CM=DM=DP=![]() ,由此可判断④.
,由此可判断④.
连接OM,
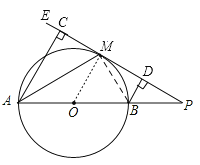
∵PE为⊙O的切线,
∴OM⊥PC,
∵AC⊥PC,
∴OM∥AC,
∴∠CAM=∠AMO,
∵OA=OM,
∠OAM=∠AMO,
∴∠CAM=∠OAM,即AM平分∠CAB,故①正确;
∵AB为⊙O的直径,
∴∠AMB=90°,
∵∠CAM=∠MAB,∠ACM=∠AMB,
∴△ACM∽△AMB,
∴![]() ,
,
∴AM2=ACAB,故②正确;
∵∠APE=30°,
∴∠MOP=∠OMP﹣∠APE=90°﹣30°=60°,
∵AB=4,
∴OB=2,
∴![]() 的长为
的长为![]() ,故③错误;
,故③错误;
∵BD⊥PC,AC⊥PC,OM⊥PC,
∴BD∥AC//OM,
∴△PBD∽△PAC,
∴![]() ,
,
∴PB=![]() PA,
PA,
又∵AO=BO,AO+BO=AB,AB+PB=PA,
∴PB=OB=AO,
又∵BD∥AC//OM,
∴PD=DM=CM,
∴OM=2BD=2,
在Rt△PBD中,PB=BO=OM=2
∴PD=![]() =
=![]() ,
,
∴CM=DM=DP=![]() ,故④正确,
,故④正确,
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】(定义)若一个四边形恰好关于其中一条对角线所在的直线对称,则我们将这个四边形叫做镜面四边形.
(理解)(1)下列说法是否正确(对的打√,错的打×)
①平行四边形是一个镜面四边形
②镜面四边形的面积等于对角线积的一半.
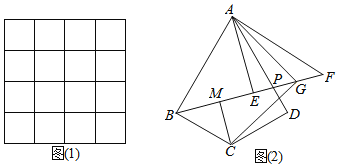
(2)如图(1),请你在4×4的网格(每个小正方形的边长为1)中画出一个镜面四边形,使它图(1)的顶点在格点上,且有一边长为![]() .
.
(应用)(3)如图(2),已知镜面四边形ABCD,∠BAD=60°,∠ABC=90°,AB≠BC,P是AD上一点,AE⊥BP的延长线上取一点F,使EF=BE,连接AF,作∠FAD的平分线AG交BF于G,CM⊥BF于M,连接CG.
①求∠EAG的度数.
②比较BM与EG的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田赛项目:跳远,跳高
;田赛项目:跳远,跳高![]() 分别用
分别用![]() 、
、![]() 表示
表示![]() .
.
![]() 该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
![]() 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).

(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
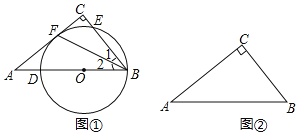
(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=![]() 在第一象限内的图象与直线y=
在第一象限内的图象与直线y=![]() x交于点D,且反比例函数y=
x交于点D,且反比例函数y=![]() 交BC于点E,AD=3.
交BC于点E,AD=3.
(1)求D点的坐标及反比例函数的关系式;
(2)若矩形的面积是24,请写出△CDE的面积(不需要写解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com