
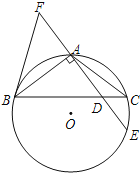
【题目】如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE⊥AB交BC于点D,交⊙O于点E,F在DA的延长线上,且AF=AD.若AF=3,tan∠ABD=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】![]()
【解析】试题分析:如图,连接BE.利用等腰三角形“三线合一”的性质得到BF=BD;然后根据圆周角定理推知∠FBA=∠ABC=∠C=∠E,BE是⊙O的直径.利用锐角三角函数的定义可以来求BE的长度.
试题解析:
如图,连接BE.
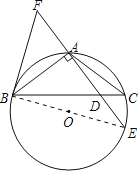
∵AF=AD,AB⊥EF,
∴BF=BD.是直径
∵AB=AC,
∴∠FBA=∠ABC=∠C=∠E.
∵tan∠ABD=![]() ,
,
∴tanE=tan∠FBA=![]() .
.
在Rt△ABF中,∠BAF=90°.
∵tan∠FBA=![]() =
=![]() ,AF=3,
,AF=3,
∴AB=4.
∵∠BAE=90°,
∴BE是⊙O的直径.
∵tanE=tan∠FBA=![]()
![]() ,AB=4,
,AB=4,
∴设AB=3x,AE=4x,
∴BE=5x,
∵3x=4,
∴BE=5x=![]() ,
,
即⊙O的直径是![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】某种油菜籽在相同条件下的发芽实验结果如表:
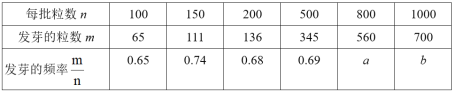
(1)a= ,b= ;
(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;
(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与![]() 轴交于点C,顶点为D,对称轴与
轴交于点C,顶点为D,对称轴与![]() 轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交
轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交![]() 轴交于点G.
轴交于点G.
(1)如图①,求直线CE的解析式和顶点D的坐标;
(2)如图①,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于![]() 轴的直线l上一点,点N是抛物线对称轴上一点,求
轴的直线l上一点,点N是抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)如图②,过点D作![]() 交
交![]() 轴于点I,将△GDI沿射线GB方向平移至
轴于点I,将△GDI沿射线GB方向平移至![]() 处,将
处,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,当旋转到一定度数时,点
,当旋转到一定度数时,点![]() 会与点I重合,记旋转过程中的
会与点I重合,记旋转过程中的![]() 为
为![]() ,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个盒子中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色.请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(+17)+(-12);
(2)10+(―![]() )―6―(―0.25);
)―6―(―0.25);
(3)(![]() )×48 ;
)×48 ;
(4)|-5-4|-5×(-2)2-1÷(-![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014河南21题)某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下降![]() 元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=5,CE=4,则⊙O的半径是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com