
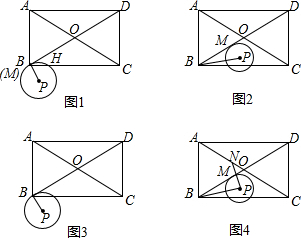
分析 发现:由四边形ABCD是矩形,得到∠BCD=90°,DC=AB=8,根据勾股定理得到BD=16,根据特殊角的三角函数值即可得到结论;
拓展:①如图1,连接PH,过点P作PE⊥BC于点E,根据切线的性质得到∠PBD=90°,根据直角三角形的性质得到BE=$\frac{\sqrt{3}}{2}$,于是得到S扇形PBH=$\frac{60π(\sqrt{3})^{2}}{360}$=$\frac{1}{2}$π,S△PBH=$\frac{3\sqrt{3}}{4}$,即可得到结论;
②如图2,当AP⊥BD时,AP有最小值,解直角三角形即可得到结论;
探究:①如图3,当点P在△BOC内时,根据切线的性质得到∠BOP=60°,求得BM=7,于是得到tan∠PBC=$\frac{\sqrt{3}}{6}$,如图4,当点P在△DOC内时,根据切线的性质得到∠DOP=30°,于是得到tan∠PBC=$\frac{2\sqrt{3}}{9}$;
②如图5,过P作直线l∥BD,作B关于直线l的对称点B′,过B′,P作直线PB′交BD于K,交AC于N,则此时PB+PN的值最小,且B′N=PB+PN,解直角三角形即可得到结论.
解答 解:发现:∵四边形ABCD是矩形,
∴∠BCD=90°,DC=AB=8,
∴BD=$\sqrt{B{C}^{2}+D{C}^{2}}$=$\sqrt{(8\sqrt{3})^{2}+{8}^{2}}$=16,
∵sin∠CBD=$\frac{DC}{BC}$=$\frac{1}{2}$,
∴∠CBD=30°,
故答案为:16,30°; 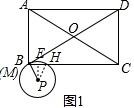 拓展:①如图1,连接PH,过点P作PE⊥BC于点E,
拓展:①如图1,连接PH,过点P作PE⊥BC于点E,
∵⊙P与线段BD相切于点B
∴∠PBD=90°
∴∠CBP=60°
∵PB=$\sqrt{3}$,
∴BE=$\frac{\sqrt{3}}{2}$,
∵PB=PH
∴∠BPH=60°,BH=$\sqrt{3}$
∴S扇形PBH=$\frac{60π(\sqrt{3})^{2}}{360}$=$\frac{1}{2}$π,S△PBH=$\frac{3\sqrt{3}}{4}$,
∴⊙P与矩形ABCD重叠部分的面积为$\frac{1}{2}$π-$\frac{3\sqrt{3}}{4}$, ②如图2,当AP⊥BD时,AP有最小值,
②如图2,当AP⊥BD时,AP有最小值,
∵AD=8$\sqrt{3}$,∠ADB=30°,
∴AM=4$\sqrt{3}$,
∴AP的最小值为5$\sqrt{3}$,
探究:①如图3,当点P在△BOC内时,
∵⊙P与AC、BD相切,
∴∠BOP=60°,
∴OM=1,
∴BM=7,
此时tan∠PBC=$\frac{\sqrt{3}}{6}$,
如图4,当点P在△DOC内时,
∵⊙P与AC、BD相切,
∴∠DOP=30°,
∴OM=3,
∴BM=11,
此时tan∠PBC=$\frac{2\sqrt{3}}{9}$,
②如图5, 过P作直线l∥BD,作B关于直线l的对称点B′,过B′,P作直线PB′交BD于K,交AC于N,
过P作直线l∥BD,作B关于直线l的对称点B′,过B′,P作直线PB′交BD于K,交AC于N,
则此时PB+PN的值最小,且B′N=PB+PN,
连接PM,
∴PM⊥BD,
∵BB′⊥l,
∴BB′⊥BD,
∴PM∥BB′,
∵∠DBC=30°,
∴∠CBB′=60°,
∴△PBB′是等边三角形,
∴∠B′=60°,
∴B′K=2BB′=4PM=4$\sqrt{3}$,
∵∠KPC=∠BPB′=60°,
∴∠ONK=90°,
∴∠NKO=∠BKP=30°,
∵MK=$\sqrt{3}$PM=3,
∴OK=8-6=2,
∴NK=$\sqrt{3}$,
∴PB+PN的最小值=B′K+NK=5$\sqrt{3}$.
点评 本题考查了矩形的性质,切线的性质,勾股定理,等边三角形的判定和性质,解直角三角形,轴对称-最小距离问题,扇形面积的计算,正确的作出辅助线构造直角三角形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )| A. | (-1,1) | B. | (-2,-1) | C. | (-3,1) | D. | (1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
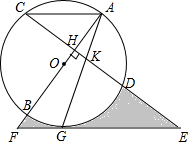 如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K、E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F.
如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K、E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )
如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个实数中,绝对值最大的一个是( )| A. | p | B. | q | C. | m | D. | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com