
 如图,AB=AD,AB⊥AD,AE⊥AC,AE=AC,连接BE,过A作AH⊥CD于H,交BE于F.求证:
如图,AB=AD,AB⊥AD,AE⊥AC,AE=AC,连接BE,过A作AH⊥CD于H,交BE于F.求证:分析 (1)根据SAS即可证明△ABC≌△ADE.
(2)连接CF.想办法证明CF=EF,BF=CF即可解决问题.
解答 证明:(1)∵AB⊥AD,AE⊥AC,
∴∠BAD=∠CAE=90°,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAD=∠DAE}\\{AC=AE}\end{array}\right.$,
∴△ABC≌△ADE.
(2)连接CF.∵△ABC≌△ADE,
∴∠AEC=ACB,
在Rt△ACE中,∠ACE+∠AEC=90°,
∴∠BCE=90°,
∵AE=AC,AH⊥CD,
∴CH=HE,
∴CF=EF,
∴∠CEF=∠ECF,
∵∠CEF+∠CBE=90°,∠ECF+∠BCF=90°,
∴∠CBF=∠BCF,
∴BF=CF,
∴BF=EF.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质,线段的垂直平分线的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会添加常用辅助线,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
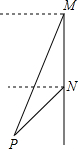 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为41.682(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为41.682(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,拟从点A修建一条小径到边BC,若要使修建小径使用的材料最少,则过点A作AD⊥BC于点D,线段AD即为所求小径的位置,这样画的理由是垂线段最短.
如图,拟从点A修建一条小径到边BC,若要使修建小径使用的材料最少,则过点A作AD⊥BC于点D,线段AD即为所求小径的位置,这样画的理由是垂线段最短.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 无解 | B. | 有一组解 | C. | 有无穷多解 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com