
【题目】如图,已知Rt△ABD中,∠A=90°,将斜边BD绕点B顺时针方向旋转至BC,使BC∥AD,过点C作CE⊥BD于点E. 
(1)求证:△ABD≌△ECB;
(2)若∠ABD=30°,BE=3,求弧CD的长.
【答案】
(1)证明:∵∠A=90°,CE⊥BD,
∴∠A=∠BEC=90°.
∵BC∥AD,
∴∠ADB=∠EBC.
∵将斜边BD绕点B顺时针方向旋转至BC,
∴BD=BC.
在△ABD和△ECB中,

∴△ABD≌△ECB
(2)解:∵△ABD≌△ECB,
∴AD=BE=3.
∵∠A=90°,∠BAD=30°,
∴BD=2AD=6,
∵BC∥AD,
∴∠A+∠ABC=180°,
∴∠ABC=90°,
∴∠DBC=60°,
∴弧CD的长为 ![]() =2π
=2π
【解析】(1)因为这两个三角形是直角三角形,根据旋转的性质得出BC=BD,由AD∥BC推出∠ADB=∠EBC,从而能证明△ABD≌△ECB;(2)由全等三角形的性质得出AD=BE=3.根据30°角所对的直角边等于斜边的一半得出BD=2AD=6,根据平行线的性质求出∠DBC=60°,再代入弧长计算公式求解即可.
【考点精析】根据题目的已知条件,利用弧长计算公式和旋转的性质的相关知识可以得到问题的答案,需要掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.
(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?
(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图填空:
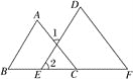
(1)∵∠1=∠A(已知),
∴_________(______________________);
(2)∵∠1=∠D(已知),
∴________(________________________);
(3)∵______=∠F(已知),
∴AC∥DF(______________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
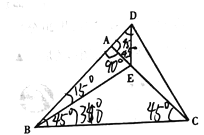
【题目】如图,在△ABC中.AB=AC.∠BAC=90![]() .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30![]() ,求∠ADC的度数.
,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:
计算代数式![]() (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的![]() (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | …… |
下面是小东计算代数式![]() (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | 2 | 1 |
|
|
|
| …… |
(1)上表是![]() (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式![]() 的值;
的值;
(2)随着x值的增大,代数式![]() 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);
(3)当x值无限增大时,代数式![]() 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;
②当﹣1≤x≤3时,y<0;
③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )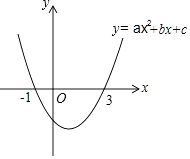
A.①②④
B.①②③
C.①④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 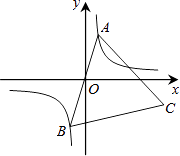
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com