
 如图,已知点A(n,6),B(6,m)在双曲线y=$\frac{6}{x}$的图象上,以AB为直径的eM与x轴交于点E(3,0)和点F,抛物线y=ax2+bx+12(a≠0)的图象经过点A、E、F.
如图,已知点A(n,6),B(6,m)在双曲线y=$\frac{6}{x}$的图象上,以AB为直径的eM与x轴交于点E(3,0)和点F,抛物线y=ax2+bx+12(a≠0)的图象经过点A、E、F.分析 (1)将两个点的坐标代入到反比例函数的解析式即可求得m和n的值;
(2)将A和点E的坐标代入二次函数的解析式即可求得a、b的值,从而确定二次函数的解析式;
(3)得到CG2+MG2=CM2后即可得到△CMG是直角三角形,且MG⊥CG,从而判定直线CG与⊙M相切.
解答  解:(1)∵A(n,6),B(6,m)在双曲线y=$\frac{6}{x}$的图象上
解:(1)∵A(n,6),B(6,m)在双曲线y=$\frac{6}{x}$的图象上
∴n=1,m=1;
(2)依题意,把A(1,6),E(3,0)代入y=ax2+bx+12中,
得$\left\{\begin{array}{l}a+b+12=6\\ 9a+3b+12=0\end{array}\right.$(4分)
解得$\left\{\begin{array}{l}a=1\\ b=-7\end{array}\right.$,
∴抛物线的解析式为:y=x2-7x+12;
(3)由(2)有抛物线解析式为y=x2-7x+12,
令x=0,则y=12,
∴C(0,12),
∵A(1,6),B(6,1)
∴M($\frac{7}{2}$,$\frac{7}{2}$),
∵点A、G关于抛物线的对称轴$x=\frac{7}{2}$对称
∴G(6,6),
连结CM,MG,AG,延长GA交y轴于点I,过M点作MN⊥AG于N,
过M点作y轴的垂线,交y轴于H点,根据勾股定理可求得:CM2=MH2+CH2=3.52+8.52=85,
CG2=GI2+CI2=62+62=72,
MG2=MN2+NG2=2.52+2.52=13,
∴CG2+MG2=CM2
∴△CMG是直角三角形,且MG⊥CG,
∴直线CG与⊙M相切.
点评 本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和反比例函数的性质.在求有关动点问题时要注意分析题意分情况讨论结果.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
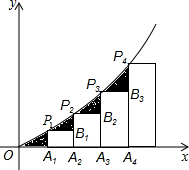 如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.
如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
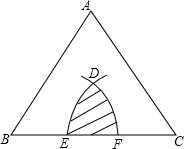 正△ABC的边长是4,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分的面积为S,当2$\sqrt{2}$≤r≤4时,S的取值范围是多少?
正△ABC的边长是4,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分的面积为S,当2$\sqrt{2}$≤r≤4时,S的取值范围是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画.
如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com