

���� ��1������CD����ͼ1�����õ���ֱ�������ε����ʵ�CD��AB��CD=AD=BD��CDƽ�֡�ACB��Ȼ��֤����ADE�ա�CDF�õ�AE=CF���Ӷ��õ�EC+CF=AC=4��
��2����DG��AC��G��DH��BC��H����ͼ2����֤��Rt��DEG��Rt��DFH�õ�$\frac{DE}{DF}$=$\frac{DG}{DH}$����������������λ�����ʵ�DG=$\frac{1}{2}$BC��DH=$\frac{1}{2}$AC����$\frac{DG}{DH}$=$\frac{BC}{AC}$������$\frac{DE}{DF}$=$\frac{BC}{AC}$��Ȼ��������������ε��ж��������жϡ�EDF�ס�BCA��
��3����DM��AC��M����ͼ3����֤��Rt��DME��Rt��ECF�õ�$\frac{DM}{CE}$=$\frac{DE}{EF}$���ٵõ�DM=$\frac{1}{2}$BC=2��AM=CM=$\frac{1}{2}$AC=$\frac{1}{2}$x�����Ÿ������еĶ���õ�tan��DEF=$\frac{EF}{DE}$=2����EF=2DE�����ǿɼ����CE=4����ME=$\frac{1}{2}$x-4�����ù��ɶ����ɵõ�DE2=$\frac{1}{4}$��x-8��2+4��Ȼ�����������������ʽ�õ�S=DE2=$\frac{1}{4}$��x-8��2+4��8��x��10���������ö��κ��������ʽ�����⣮
��� �⣺��1�� ����CD����ͼ1��
����CD����ͼ1��
��AC=BC=4����ACB=90�㣬
���ACBΪ����ֱ�������Σ�
��D��ΪAB���е㣬
��CD��AB��CD=AD=BD��CDƽ�֡�ACB��
���A=45�㣬��ACD=��BCD=45�㣬
�ߡ�EDF=90�㣬����EDC+��FDC=90�㣬
����EDC+��ADE=90�㣬
���ADE=��CDF��
�ڡ�ADE�͡�CDF��
$\left\{\begin{array}{l}{��A=��DCF}\\{AD=CD}\\{��ADE=��CDF}\end{array}\right.$��
���ADE�ա�CDF��
��AE=CF��
��EC+CF=EC+AE=AC=4��
�ʴ�Ϊ4��
��2�����ƣ�
��DG��AC��G��DH��BC��H����ͼ2�����ı���DGCHΪ���Σ�
���GDH=90�㣬����GDF+��FDH=90�㣬
�ߡ�EDF=90�㣬����EDG+��GDF=90�㣬
���EDG=��FDH��
��Rt��DEG��Rt��DFH��
��$\frac{DE}{DF}$=$\frac{DG}{DH}$��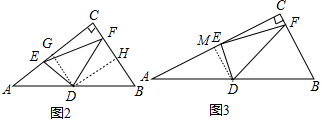
�ߵ�DΪAB���е㣬
��DG=$\frac{1}{2}$BC��DH=$\frac{1}{2}$AC��
��$\frac{DG}{DH}$=$\frac{BC}{AC}$��
��$\frac{DE}{DF}$=$\frac{BC}{AC}$����$\frac{DE}{BC}$=$\frac{DF}{AC}$��
����EDF=��C=90�㣬
���EDF�ס�BCA��
��3����DM��AC��M����ͼ3��
�ߡ�DEF=90�㣬
���DEM+��CEF=90�㣬
����DEM+��DME=90�㣬
���CEF=��DME��
��Rt��DME��Rt��ECF��
��$\frac{DM}{CE}$=$\frac{DE}{EF}$��
�ߵ�DΪAB���е㣬
��DM=$\frac{1}{2}$BC=2��AM=CM=$\frac{1}{2}$AC=$\frac{1}{2}$x��
��tan��DEF=$\frac{EF}{DE}$=2����EF=2DE��
��$\frac{DM}{CE}$=$\frac{1}{2}$��
��CE=4��
��ME=MC-CE=$\frac{1}{2}$x-4��
��Rt��DME��DE2=22+��$\frac{1}{2}$x-4��2=$\frac{1}{4}$��x-8��2+4��
��S=$\frac{1}{2}$DE•EF=$\frac{1}{2}$DE•2DE=DE2=$\frac{1}{4}$��x-8��2+4��8��x��10����
��x��8ʱ��S��x�����������
�൱x=10ʱ��Sȡ���ֵ�����ֵΪ$\frac{1}{4}$��10-8��2+4=5��
���� ���⿼���������ε��ۺ��⣺�������ն��κ��������ʡ�����ֱ�������ε����ʺ����������ε��ж������ʣ�ͨ����ƽ���߹��������������ǽ������Ĺؼ���ͬʱѧ���ô���ʽ��ʾ�߶�֮��Ĺ�ϵ��


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
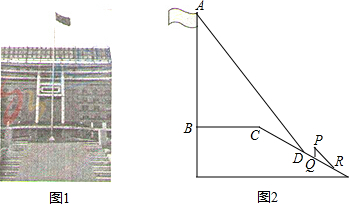
 ��ͼ����ƽ��ֱ������ϵ�ڣ���OΪ����ԭ�㣬������A��-4��4����������y=$\frac{1}{k}$��x+2����x+a����x�Ḻ�����ڵ�B����x���������ڵ�C����y���ڵ�D��0��-2����
��ͼ����ƽ��ֱ������ϵ�ڣ���OΪ����ԭ�㣬������A��-4��4����������y=$\frac{1}{k}$��x+2����x+a����x�Ḻ�����ڵ�B����x���������ڵ�C����y���ڵ�D��0��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
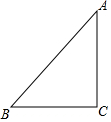 ��ͼ����֪��ABC�У���C=90�㣬AC=BC=$\sqrt{2}$������ABC�Ƶ�A˳ʱ�뷽����ת60�㵽��AB��C���λ�ã�����C��B��
��ͼ����֪��ABC�У���C=90�㣬AC=BC=$\sqrt{2}$������ABC�Ƶ�A˳ʱ�뷽����ת60�㵽��AB��C���λ�ã�����C��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ѧУ�ݽ������У�ʮ��ѡ�ֵijɼ�ͳ��ͼ��ͼ��ʾ������10��ѡ�ֳɼ���ƽ������88.5�֣�
��ѧУ�ݽ������У�ʮ��ѡ�ֵijɼ�ͳ��ͼ��ͼ��ʾ������10��ѡ�ֳɼ���ƽ������88.5�֣��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com