
 ŌĶĮĻĀĢā¼°Ņ»Ī»Ķ¬Ń§µÄ½ā“š¹ż³Ģ£ŗČēĶ¼£¬ABŗĶCDĻą½»ÓŚµćO£¬ĒŅOA=OB£¬”ĻA=”ĻC£¬ÄĒĆ“”÷AODÓė”÷COBČ«µČĀš£æČōČ«µČ£¬ŹŌŠ“³öÖ¤Ć÷¹ż³Ģ£¬Čō²»Č«µČ£¬ĒėĖµĆ÷ĄķÓÉ
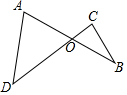
ŌĶĮĻĀĢā¼°Ņ»Ī»Ķ¬Ń§µÄ½ā“š¹ż³Ģ£ŗČēĶ¼£¬ABŗĶCDĻą½»ÓŚµćO£¬ĒŅOA=OB£¬”ĻA=”ĻC£¬ÄĒĆ“”÷AODÓė”÷COBČ«µČĀš£æČōČ«µČ£¬ŹŌŠ“³öÖ¤Ć÷¹ż³Ģ£¬Čō²»Č«µČ£¬ĒėĖµĆ÷ĄķÓÉ·ÖĪö Į½½Ē¼Š±ß¶ŌÓ¦ĻąµČµÄĮ½øöČż½ĒŠĪČ«µČ¼“æÉÅŠ¶Ļ£®
½ā“š ½ā£ŗÕāĪ»Ķ¬Ń§µÄ½ā·Ø“ķĪó£®
ŅņĪŖĮ½½Ē¼Š±ß¶ŌÓ¦ĻąµČµÄĮ½øöČż½ĒŠĪČ«µČ£®
±¾ĢāÖŠ£¬”ĻAÓė”ĻAODµÄ¼Š±ßŹĒOA£¬”ĻCÓė”ĻBOCµÄ¼Š±ßŹĒOC£¬
ŅņĪŖOA”ŁOC£¬ĖłŅŌ²»ÄÜÖ¤Ć÷Į½Čż½ĒŠĪČ«µČ£®
µćĘĄ ±¾Ģāæ¼²éČ«µČČż½ĒŠĪµÄÅŠ¶Ļ£¬½āĢāµÄ¹Ų¼üŹĒĄķ½āĮ½½Ē¼Š±ß¶ŌÓ¦ĻąµČµÄĮ½øöČż½ĒŠĪČ«µČ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬”ĻAOB=90”ć£¬OA=OB£¬Ö±Ļßl¾¹żµćO£¬·Ö±š¹żA£¬BĮ½µć×÷AC”Ķl£¬BD”Ķl£¬“¹×ć·Ö±šĪŖµćC£¬D£®ĒóÖ¤£ŗAC=OD£®
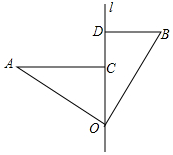
ČēĶ¼£¬”ĻAOB=90”ć£¬OA=OB£¬Ö±Ļßl¾¹żµćO£¬·Ö±š¹żA£¬BĮ½µć×÷AC”Ķl£¬BD”Ķl£¬“¹×ć·Ö±šĪŖµćC£¬D£®ĒóÖ¤£ŗAC=OD£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬”÷ABCŗĶ”÷ADE¶¼ŹĒµČŃüČż½ĒŠĪ£¬ĒŅ”ĻBAC=90”ć£¬”ĻDAE=90”ć£¬B£¬C£¬DŌŚĶ¬Ņ»Ö±ĻßÉĻ£®
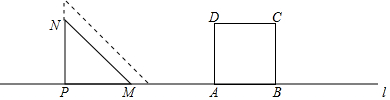
ČēĶ¼£¬”÷ABCŗĶ”÷ADE¶¼ŹĒµČŃüČż½ĒŠĪ£¬ĒŅ”ĻBAC=90”ć£¬”ĻDAE=90”ć£¬B£¬C£¬DŌŚĶ¬Ņ»Ö±ĻßÉĻ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚ”ŃOÖŠ£¬ABĪŖÖ±¾¶£¬µćC£¬DĪŖŌ²ÉĻĮ½µć£¬Į¬½ÓAC£¬BC£¬¹żµćC×÷ABµÄ“¹Ļߣ¬“¹×ćĪŖµćF£¬¹żµćD×÷”ŃOµÄĒŠĻß½»FCµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓAD½»CFÓŚµćG£®
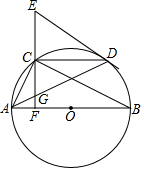
ČēĶ¼£¬ŌŚ”ŃOÖŠ£¬ABĪŖÖ±¾¶£¬µćC£¬DĪŖŌ²ÉĻĮ½µć£¬Į¬½ÓAC£¬BC£¬¹żµćC×÷ABµÄ“¹Ļߣ¬“¹×ćĪŖµćF£¬¹żµćD×÷”ŃOµÄĒŠĻß½»FCµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓAD½»CFÓŚµćG£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\frac{\sqrt{2017}}{{2}^{2016}}$ | B£® | -$\frac{\sqrt{2017}}{{2}^{2016}}$ | C£® | $\frac{\sqrt{2018}}{{2}^{2017}}$ | D£® | -$\frac{\sqrt{2018}}{{2}^{2017}}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
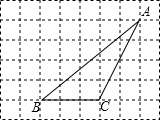 ČēĶ¼ĖłŹ¾£¬ŌŚ±ß³¤ĪŖ1øöµ„Ī»³¤¶ČµÄÕż·½ŠĪĶųøńÖŠ£¬×÷³ö”÷ABCµÄ±ßBCÉĻµÄøߣ¬²¢¼ĘĖć”÷ABCµÄĆ껿£®
ČēĶ¼ĖłŹ¾£¬ŌŚ±ß³¤ĪŖ1øöµ„Ī»³¤¶ČµÄÕż·½ŠĪĶųøńÖŠ£¬×÷³ö”÷ABCµÄ±ßBCÉĻµÄøߣ¬²¢¼ĘĖć”÷ABCµÄĆ껿£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com