
【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形. 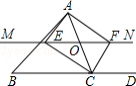
A.30°
B.45°
C.60°
D.90°
【答案】D
【解析】解:过点E,F作EH⊥BD,FG⊥BD, ∵CE,CF为∠ACB,∠ACD的角平分线,
∴∠ECF=90°.
∵MN∥BC,
∴∠FEC=∠ECH,
∵∠ECH=∠ECO,
∴∠FEC=∠ECO,
∴OE=OC.
同理OC=OF,
∴OE=OF,
∵点O运动到AC的中点,
∴OA=OC,
∴四边形AECF为一矩形,
若∠ACB=90°,则CE=CF,
∴四边形AECF为正方形.
故选:D.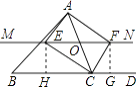
【考点精析】解答此题的关键在于理解三角形的外角的相关知识,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对正方形的判定方法的理解,了解先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我县某初中学校举办“经典诵读”比赛,13名学生进入决赛,他们所得分数互不相同,比赛共设7个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )
A. 众数B. 中位数C. 平均数D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.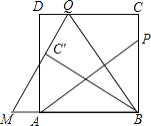
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
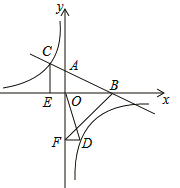
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com