
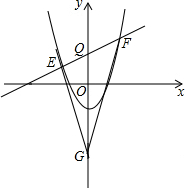
 如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由. 分析 结论:不存在.假设存在点G,使EQ•FG=FQ•EG,作QN⊥GE于N,QF⊥GF于M.只要说明与已知条件矛盾即可解决问题.
解答 解:不存在.
理由:假设存在点G,使EQ•FG=FQ•EG,作QN⊥GE于N,QF⊥GF于M.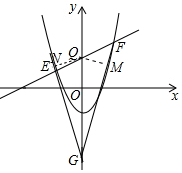
∴$\frac{EQ}{QF}$=$\frac{GE}{GF}$=$\frac{{S}_{△EQG}}{{S}_{△FGQ}}$=$\frac{\frac{1}{2}•EG•QN}{\frac{1}{2}•FG•QM}$,
∴QN=QM,
∴∠QGE=∠GQF,
∵抛物线y=$\frac{1}{2}$x2-2关于y轴对称,∠EGF关于y轴对称,
∴E、F关于y轴对称,
∴EF∥x轴,这与已知条件矛盾,
∴假设不成立,
∴不存在.
点评 本题考查二次函数图象上的点的坐标特征、角平分线的判定定理、三角形的面积一次函数的应用等知识,解题的关键是学会利用反证法解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 正面朝上的概率大 | B. | 反面朝上的概率大 | ||
| C. | 正面朝上和反面朝上的概率一样大 | D. | 一定是反面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A和点B都在反比例函数y=$\frac{6}{x}$的图象上,且线段AB过原点,过点A作x轴的垂线段,垂足为C,P是线段OB上的动点,连接CP.设△ACP的面积为S,则下列说法正确的是( )
如图,点A和点B都在反比例函数y=$\frac{6}{x}$的图象上,且线段AB过原点,过点A作x轴的垂线段,垂足为C,P是线段OB上的动点,连接CP.设△ACP的面积为S,则下列说法正确的是( )| A. | S>3 | B. | S>6 | C. | 3≤S≤6 | D. | 3<S≤6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{m}$ | B. | $\sqrt{m+2}$ | C. | $\sqrt{{m}^{2}+2}$ | D. | $\sqrt{-20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com