
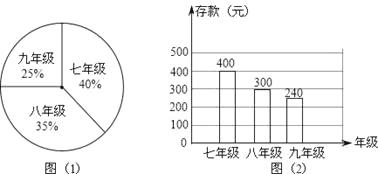
【题目】为了帮助贫困失学儿童,宿迁市团委发起“爱心储蓄”活动,鼓励学生将自己的压岁钱和零花钱存入银行,定期一年,到期后取回本金,而把利息捐赠给贫困失学儿童.某中学共有学生1200人,图1是该校各年级学生人数比例分布的扇形统计图,图2是该校学生人均存款情况的条形统计图.
(1)求该学校的人均存款数;
(2)已知银行一年定期存款的年利率是2.25%(“爱心储蓄”免收利息税),且每351元能提供给1位失学儿童一年的基本费用,那么该学校一学年能够帮助多少位失学儿童?
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 的直径
的直径![]() ,半径
,半径![]() ,
,![]() 为
为![]() 上一动点(不包括
上一动点(不包括![]() 两点),
两点),![]() ,垂足分别为
,垂足分别为![]() .
.

(1)求![]() 的长.
的长.
(2)若点![]() 为
为![]() 的中点,
的中点,
①求劣弧![]() 的长度,
的长度,
②者点![]() 为直径
为直径![]() 上一动点,直接写出
上一动点,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润![]() (万元)与月份
(万元)与月份![]() 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )

A.4月份的利润为![]() 万元
万元
B.污改造完成后每月利润比前一个月增加![]() 万元
万元
C.治污改造完成前后共有![]() 个月的利润低于
个月的利润低于![]() 万元
万元
D.9月份该厂利润达到![]() 万元
万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .点
.点![]() 在函数图像上,
在函数图像上,![]() 轴,且
轴,且![]() ,直线
,直线![]() 是抛物线的对称轴,
是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求![]() 、
、![]() 的值;
的值;
(2)如图①,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)如图②,动点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线分别与
轴的垂线分别与![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等,且线段
的面积相等,且线段![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类记为A;音乐类记为B;球类记为C;其他类记为D.根据调查结果发现该班每个学生都进行了等级且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
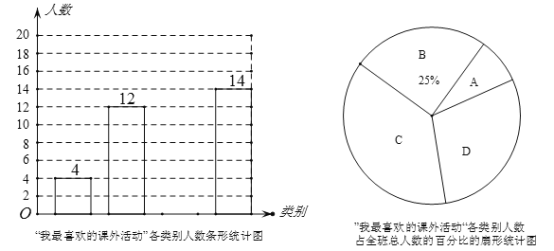
(1)七年级(1)班学生总人数为_______人,扇形统计图中D类所对应扇形的圆心角为_____度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
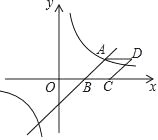
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
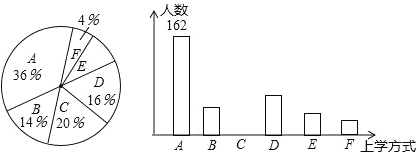
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
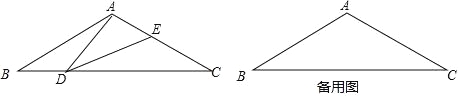
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蛋糕房推出一种新品蛋糕,每个成本为50元经过一段时间的售卖发现,当单价定为90元的时候,可卖100个,而单价每降低1元,就会多卖出10个
(1)写出销售量![]() (个)与销售单价
(个)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)若设销售这种蛋糕的利润为![]() (元),请写出
(元),请写出![]() 与销售单价
与销售单价![]() (元)之间的函数关系式,并计算当销售单价定为多少元时该蛋糕房可获得最大利润(不需要计算最大利润);
(元)之间的函数关系式,并计算当销售单价定为多少元时该蛋糕房可获得最大利润(不需要计算最大利润);
(3)若想尽可能地降低成本,并使该蛋糕房获利6000元,应将销售单价定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com