
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E. 
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S.
【答案】
(1)解:∵∠D=60°,
∴∠B=60°(圆周角定理),
又∵AB=6,
∴BC=3,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OE⊥AC,
∴OE∥BC,
又∵点O是AB中点,
∴OE是△ABC的中位线,
∴OE= ![]() BC=
BC= ![]()
(2)解:连接OC,

则易得△COE≌△AFE,
故阴影部分的面积=扇形FOC的面积,
S扇形FOC= ![]() =
= ![]() π.
π.
即可得阴影部分的面积为 ![]() π
π
【解析】(1)根据∠D=60°,可得出∠B=60°,继而求出BC,判断出OE是△ABC的中位线,就可得出OE的长;(2)连接OC,将阴影部分的面积转化为扇形FOC的面积.
【考点精析】认真审题,首先需要了解含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】周末,小明,小红等同学随父母一同去某景点旅游,在购买门票时,小明和小红有图1所示的对话,根据图2的门票票价和图1所示的对话内容完成下列问题.
(1)他们一共去了几个成人几个学生?
(2)请你帮他们算一算,用哪种方式买票更省钱,省多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式![]() x+y+1的值.
x+y+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界读书日,新华书店矩形购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元一律八折;③一次性购书200元以上一律打六折.小丽在这次活动中,两次购书总共付款190.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2017次相遇在边( )上.

A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
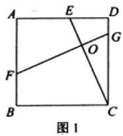
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=![]() =5050.
=5050.
(1)补全例题![]() 解题过程;
解题过程;
(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com