
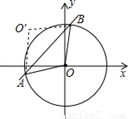
如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点![]() .
.
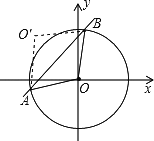
(1)求证:四边形![]() 是菱形;
是菱形;
(2)当点O′落在⊙O上时,求b的值.
|
分析:(1)根据轴对称得出直线y=x+b是线段 (2)设直线y=x+b与x轴、y轴的交点坐标分别是N(-b,0),P(0,b),得出等腰直角三角形ONP,求出OM⊥NP,求出MP=OM=1,根据勾股定理求出即可. 解答:(1)证明:∵点O关于直线y=x+b的对称, ∴直线y=x+b是线段OO′D的垂直平分线, ∴AO= 又∵OA,OB是⊙O的半径, ∴OA=OB, ∴AO= ∴四边形 (2)解:如图,当点 ∵设直线y=x+b与x轴、y轴的交点坐标分别是N(-b,0),P(0,b), ∴△ONP为等腰直角三角形, ∴∠ONP=45°, ∵四边形 ∴OM⊥PN, ∵∠ONP=45°=∠OPN, ∴OM=PM=MN=1, 在Rt△POM中,由勾股定理得:OP= 即b=
点评:本题考查了一次函数,等腰直角三角形,勾股定理,菱形的判定等知识点的应用,主要考查学生运用定理进行推理的能力,注意:图形和已知条件的结合,题目比较典型,难度也适中,是一道比较好的题目. |
|
一次函数综合题;勾股定理;等腰直角三角形;菱形的判定. |


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
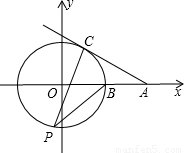
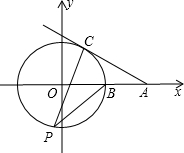 (2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )
(2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )查看答案和解析>>
科目:初中数学 来源: 题型:
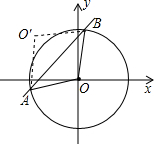 (2012•连云港)如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,
(2012•连云港)如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏连云港卷)数学(带解析) 题型:解答题
如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,
(1)求证:四边形OAO′B是菱形;
(2)当点O′落在⊙O上时,求b的值.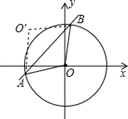
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏连云港卷)数学(解析版) 题型:解答题
如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,
(1)求证:四边形OAO′B是菱形;
(2)当点O′落在⊙O上时,求b的值.
查看答案和解析>>
科目:初中数学 来源:2012年湖北省十堰市郧县中考数学三模试卷(解析版) 题型:选择题


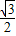

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com