
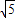 分米,CD=
分米,CD=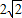 分米,梯形的高是2分米”.请你计算裁得的梯形ABCD中BC边的长度?
分米,梯形的高是2分米”.请你计算裁得的梯形ABCD中BC边的长度?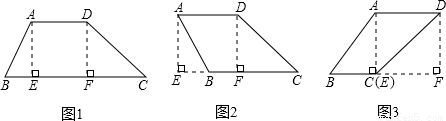
 分米,CD=
分米,CD=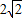 分米,
分米,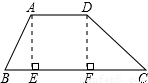
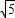 分米,AE=2分米,
分米,AE=2分米, =
= =1,
=1,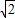 分米,DF=2分米,
分米,DF=2分米, =2分米,
=2分米,

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010年黑龙江省森工总局初中毕业学业考试数学试卷(解析版) 题型:解答题
 (2010•牡丹江)如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足
(2010•牡丹江)如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足 .
.查看答案和解析>>
科目:初中数学 来源:2010年黑龙江省森工总局初中毕业学业考试数学试卷(解析版) 题型:选择题





查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《四边形》(07)(解析版) 题型:解答题
 (2010•牡丹江)如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足
(2010•牡丹江)如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足 .
.查看答案和解析>>
科目:初中数学 来源:2010年黑龙江省牡丹江市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com